Décompositions en éléments simples

[guigui777]

Voilà ma question comment fait-on en pratiques pour faire des décompositions en éléments simples à l'aide de DL.

Avec l'exemple: F(x) 1/(x-1)X(x+1)^3 ?
pour info, on me dit de faire le DL de g(x)= f(x-1)... pourquoi? et comment poursuivre?

[Isomorphisme]

Bonjour,

C'est très simple. Ta décomposition doit être de la forme :

avec à déterminer.

1 est un pôle simple, donc c'est le cas le plus simple. Tu multiplies par 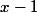et tu fais tendre vers 1. Tu trouves donc
En effet, tu as d'une part :

et d'autre part :

Et en faisant tendre vers 1 tu trouves par identification.

Pour les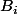 c'est le même raisonnement sauf que -1 est pôle triple. On multiplie donc par et on fait tendre vers -1 . Il vient :


Par ailleurs, tu as aussi . Pour se faciliter la vie, on fait une petite translation (changement de variable quand tend vers -1, tend vers 0) ce qui donne d'une part :

et d'autre part :


Mais quand tu fais tendre vers 0, tu t'aperçois que tu ne peux déterminer que .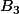
Par conséquent, pour trouver les et par identification, il suffit d'écrire le DL à l'ordre 2 au voisinage de 0 de . Et tu conclues. Et tu dois trouver (sauf erreur) :

Voilà.