Bonjour ,je cherche la décomposition des polynômes suivant dans R et C :
(X^3-8) = ( X-2)(X²+2X+4) dans R
(X-2)(X+iRacine3+1)(X+(-iracine3)) dans C
(X^4+1) = (X²+1)(X²+1) dans R
(x+i)(x-i)(x+i)(x-i) dans C
(X^6+1) = (X²+1)(X^4-X²+1) dans R
(X+i)(X-i)(X+(1/2+iRacine 3/2))(X+(-1/2-iRacine 3/2))(X+(1/2-iRacine 3/2))(X+(-1/2+iRacine 3/2)) dans C
(X^12-1)=(X²-1)(X^4+X²+1)(X²+1)(X^4-X²+1) dans R mais je suis bloqué dans C , mais je suis pas sur pour le reste aussi .
Merci :)
Décomposition d'un polynôme
8 messages
- Page 1 sur 1
Autre erreur (de nature différente) :
(X^6+1) = (X²+1)(X^4-X²+1) n'est surement pas la décomposition en facteurs irréductibles dans R vu que les seuls polynômes iréductibles sur R sont ceux du premier degré et ceux du second degré à discriminant strictement négatif.
Vu la tête des truc que tu as à factoriser, je pense que l'idée de l'exo, c'est de commencer par chercher les factorisations dans C puis d'en déduire les factorisations dans R (comment ?)
En effet, tout tes polynômes sont de la forme avec
avec  constant. Factoriser un polynôme dans C, ça revient à trouver ces racines (dans C évidement) et, dans ce cas, ça revient à chercher les racines n-ièmes du complexe
constant. Factoriser un polynôme dans C, ça revient à trouver ces racines (dans C évidement) et, dans ce cas, ça revient à chercher les racines n-ièmes du complexe  .
.
Tu as forcément vu en cours comment faire (sinon on ne t'aurais pas donné un tel exercice...)
Résumé :
1) Chercher les 3 racines cubiques de 8 dans C.
2) Chercher les 4 racines quatrièmes de -1 dans C.
3) Chercher les 6 racines sixièmes de -1 dans C.
4) Chercher les 12 racines douxièmes de 1 dans C.
(X^6+1) = (X²+1)(X^4-X²+1) n'est surement pas la décomposition en facteurs irréductibles dans R vu que les seuls polynômes iréductibles sur R sont ceux du premier degré et ceux du second degré à discriminant strictement négatif.
Vu la tête des truc que tu as à factoriser, je pense que l'idée de l'exo, c'est de commencer par chercher les factorisations dans C puis d'en déduire les factorisations dans R (comment ?)
En effet, tout tes polynômes sont de la forme
Tu as forcément vu en cours comment faire (sinon on ne t'aurais pas donné un tel exercice...)
Résumé :
1) Chercher les 3 racines cubiques de 8 dans C.
2) Chercher les 4 racines quatrièmes de -1 dans C.
3) Chercher les 6 racines sixièmes de -1 dans C.
4) Chercher les 12 racines douxièmes de 1 dans C.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonsoir
La formule du produit de deux nombres complexes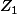 et
et 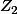 est plus simple si l'on écrit
est plus simple si l'on écrit 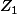 et
et 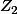 sous forme exponentielle.
sous forme exponentielle.
Si et
et  , alors
, alors }) .
.
Cette formule se généralise au cas d'un produit de n facteurs:}) .
.
On déduit que pour entier,
entier,  .
.
Revenons aux équations de la forme . En écrivant
. En écrivant  sous forme exponentielle
sous forme exponentielle
}) où
où  , on aura
, on aura },\,\,k \in \mathbb{Z}) .
.
On donc et
et  d'où
d'où  et
et  .
.
En prenant , on obtient les
, on obtient les  racines distinctes de l'équation
racines distinctes de l'équation  ,
,
}=\sqrt[n]{|a|}\left(\cos\(\frac{\phi}{n}+\frac{2k\pi}{n})\,+\,i\,\sin(\frac{\phi}{n}+\frac{2k\pi}{n}) \right))
feliraf a écrit:Je vois ce que vous avez parlé , oui j'ai vu en cours mais justement j'ai pas compris comment on fait , vous pouvez m'expliqué avec l'exemple de x^6+1
La formule du produit de deux nombres complexes
Si
Cette formule se généralise au cas d'un produit de n facteurs:
On déduit que pour
Revenons aux équations de la forme
On donc
En prenant
feliraf a écrit:Je vois ce que vous avez parlé , oui j'ai vu en cours mais justement j'ai pas compris comment on fait , vous pouvez m'expliqué avec l'exemple de x^6+1
Pour résoudre un truc du style
Ensuite tu dit que le
Tu récrit ton équation avec ces nouvelles données/inconnues et tu utilise le fait que deux complexes non nuls sont égaux ssi ils ont même module et même argument à 2k.pi prés (k dans Z).
A toi...
EDIT (ou à deltab... :lol3:)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
