Bonjour à tous : :happy3:
J'ai du mal à comprendre ce qui se suit :
Soit

un corps qui contient

et

.
Soit
 = P_1 (X,Y) ... P_s (X,Y) $)
la factorisation de
 $)
dans

.
Notons :
 = a_{m,i}(X) Y^{m_{i}} + ... + a_{0,i}(X) $)
les facteurs de
 $)
dans

.
Alors :

:
 \in \overline{\mathbb{K}} $)
.
En effet :
 $)
est à coefficients dans
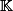
, ses racines sont donc des éléments de

, et donc :
 \in \overline{\mathbb{K}} $)
. de ce fait :
 \in \overline{\mathbb{K}}[X] $)
. Pour voir celà, il suffit d'exprimer
 $)
après une interpolation en des points de
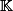
. En effet, nous exprimons des coefficients de
 $)
comme etant solutions d'un système de Vandermonde dans
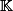
et avec pour second membre in vecteur à coefficients dans

.
Ainsi, nous obtenons

. Donc, même si nous pronons un corps contenant

, nous n'obtiendrons pas de nouveaux facteurs, celà siginife en particulier, que si
 \in \mathbb{Q} $)
, alors factoriser

dans

revient à factoriser

dans

.
Question :
Merci de m'aider à comprendre ce texte qui m'est difficile un peu :
On avance dans la lecture de ce texte à partir du sommet sans bruler les étapes :
 $)
: Je ne comprends pas le passage suivant :
il suffit d'exprimer
 $)
après une interpolation en des points de
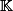
, En effet, nous exprimons des coefficients de
 $)
comme etant solutions d'un système de Vandermonde dans
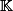
et avec pour second membre in vecteur à coefficients dans

.
Bon, on repond d'abord, à cette question, après on passe à la suite !
Merci d'avance ! :happy3:
