Salut,
Pour le MimeTeX (c'est pas vraiment du LaTeX),
clique ici pour voir le tutoriel.
Sinon, effectivement, comme
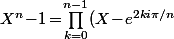)
n'a que des racines simples, la théorie concernant les décompositions en éléments simples nous dit qu'il existe

tels que
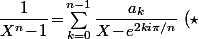)
.
Ensuite,
et comme toujours lorsque l'on a affaire à des racines simples, le plus simple pour calculer les coeff.

, c'est de multiplier les deux cotés de l'équation
)
par

puis de faire tendre

vers

.
A droite, on a

dont tout les termes tendent trivialement vers 0 (lorsque

vers

) sauf celui où

qui vaut

et, en regardant le terme de gauche, ça signifie que
-P(x_o)}\!=\!\dfrac{1}{P'(x_o)})
avec

et
\!=\!x^n-1)
(donc
\!=\!0)
)
Et c'est évidement une méthode
à connaitre absolument vu que c'est (quasi) systématiquement la plus simple pour trouver les coeffs. dans le cas de racines simples et que cette même idée de multiplier une équation par x-xo puis de faire tendre x->xo sert très souvent dans des contextes "un peu du même style".

