Décomposition en éléments simples

par **Muze** » 08 Sep 2006, 18:23

Bonjour,
Je bloque complètement sur un problème d'un ancien examen :
On doit calculer l'intégrale indéfinie

Donc logiquement on devrait avoir un truc du style :

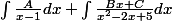
J'ai du essayer 10 fois de résoudre le système, j'arrive pas... Soit je suis un boulet, soit j'ai dû faire une erreur dans mon raisonnement!! :briques:

Merci de votre aide...

par **abcd22** » 08 Sep 2006, 18:42

Bonjour,
Si on a

, pour trouver A on multiplie l'égalité par

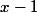
puis on remplace x par 1 : on trouve

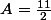
. Pour B, si on multiplie cette fois par x et qu'on fait tendre x vers l'infini, on trouve 3 = A + B et on en déduit que

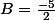
. Il ne manque plus C, pour le trouver il suffit de remplacer x par une valeur quelconque autre que 1, par exemple en prenant 0 on trouve

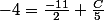
d'où

. En général pour les décompositions en éléments simples c'est plus rapide de faire comme ça que de remettre au même dénominateur et résoudre un système linéaire.

par **Muze** » 08 Sep 2006, 19:10

Merci beaucoup!
En effet j'ai raisonné en mettant tout au même dénominateur et je n'y suis pas arrivée.
Par contre je me demande encore quel est le raisonnement à faire si on met tout au même dénominateur, j'ai dû essayer une heure et je n'y suis pas arrivée... :marteau:

par **abcd22** » 08 Sep 2006, 19:24

Quand on remet au même dénominateur on obtient

, on identifie les coefficients, ce qui donne un système de 3 équations à 3 inconnues :

,

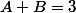
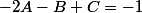
et

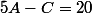
, on résout le système et on doit trouver pareil que ce que j'ai mis dans le message précédent.

par **Muze** » 08 Sep 2006, 19:39

J'ai bien trouvé ce système, mais j'arrive pas à le résoudre... :cry:

par **abcd22** » 08 Sep 2006, 20:04

J'ai pas essayé mais les valeurs que j'ai données marchent. :happy3:
Bon si on met les équations dans l'ordre :
-2A - B + C = -1 (L1)
A + B = 3 (L2)
5A - C = 20 (L3)
Pour pouvoir résoudre il suffit de modifier la 3e équation pour avoir un système triangulaire.
On remplace donc L3 par L3 + L1 pour éliminer C, et on a le système :
2A - B + C = -1 (L1)
A + B = 3 (L2)
7A - B = 19 (L3')
Pour éliminer le B de L3' on remplace L3' par L3' + L2, ce qui donne :
2A - B + C = -1 (L1)
A + B = 3 (L2)
8A = 22 (L3'')
et on peut trouver A, puis B, puis C.

par **nekros** » 08 Sep 2006, 20:16

Bonsoir tout le monde,

Muze, tu peux aller voir ce lien

A+

par **Muze** » 08 Sep 2006, 20:49

Merci beaucoup à vous tous...!

par **Muze** » 08 Sep 2006, 21:05

Juste, il n'y aurait pas une petite erreur quand tu as remplacé L3 par L3+L1?
On devrait avoir normalement 3A-B = 19 non?

par **abcd22** » 08 Sep 2006, 21:07

Muze a écrit:Juste, il n'y aurait pas une petite erreur quand tu as remplacé L3 par L3+L1?
On devrait avoir normalement 3A-B = 19 non?

Si, effectivement, il y a une erreur.

par **Muze** » 08 Sep 2006, 21:16

Bon, finalement je suis arrivée à résoudre ce système, mais c'est un peu pénible de le résoudre linéairement.
En tout cas merci à vous tous pour votre aide :D

Décomposition en éléments simples

Décomposition en éléments simples

Qui est en ligne