Decomposition elements simples
14 messages
- Page 1 sur 1
decomposition elements simples
bonjour, besoin d'un tit coup de main svp..
j'arrive pas a decomposé :
1 / (p-1)(p²-1)
quelqu'un peut m'aider siouplay ??
j'arrive pas a decomposé :
1 / (p-1)(p²-1)
quelqu'un peut m'aider siouplay ??
pas de cours pour moi, je bosse pour rattraper une entrée en école en CIF.
en gros mes cours, c'est ce que je trouve sur le net.
j'en ai deja fait et des bien plus dure a priorie, mais la ??
j'ai essayé : a/ (p+1) + b/ (P-1) + c/(p-1) et je trouve une egalité du type A+A=0 et -A-A=1 ???
j'ai essayé : a/ (p+1) + b/ (P-1) + c/(P-1)²
pas plus de succes, je cherche vraiment la forme de la décomposition..
un tit coup de main..
en gros mes cours, c'est ce que je trouve sur le net.
j'en ai deja fait et des bien plus dure a priorie, mais la ??
j'ai essayé : a/ (p+1) + b/ (P-1) + c/(p-1) et je trouve une egalité du type A+A=0 et -A-A=1 ???
j'ai essayé : a/ (p+1) + b/ (P-1) + c/(P-1)²
pas plus de succes, je cherche vraiment la forme de la décomposition..
un tit coup de main..
pour info, c'est du laplace
la méthode de résolution qui m'a été donnée et de passer transformer l'équation d'origine en un produit de convolution en espace réel, je voudrais décomposer ça en éléments simples pour comparer le résultat que j'obtiendrais, je pense que je devrais arriver au meme résultat de cette manière
la méthode de résolution qui m'a été donnée et de passer transformer l'équation d'origine en un produit de convolution en espace réel, je voudrais décomposer ça en éléments simples pour comparer le résultat que j'obtiendrais, je pense que je devrais arriver au meme résultat de cette manière
salut,
ta fraction s'écrit
s'écrit (p-1)(p+1)})
On a donc
^2(p+1)})
je note X au lieu de p
^2(X+1)}\\)
La decomp en ES est de la forme
^2} + \frac{d}{X+1})
Avec a, b, c et d dans R et a determiner.
Pour d, c'est easy, tu multiplies les deux membres par X+1 et tu évalues en X = -1.
Pour déterminer a b et c, ya ptet plus académique mais jme rappele que de ca...
Tu peux tout multiplier par (X-1)^2 et évaluer en X = 1, tu détermines alors leq
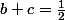
Tu peux tout multiplier par (X-1) et faire tendre X vers l'infini tu obtiens alors
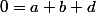
(avec d qu'on connait)
Et il faut une derniere pour avoir un systeme de trois eq a trois inconnues (a,b,c) on peut evaluer en un X quelconque (enfin, pas prendre un pole quand même) pis on DOIT avoir legalité. Donc en X=0 par exemple, on obtient
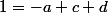
cqui devrait permettre de déterminer a, b et c
ta fraction
On a donc
je note X au lieu de p
La decomp en ES est de la forme
Avec a, b, c et d dans R et a determiner.
Pour d, c'est easy, tu multiplies les deux membres par X+1 et tu évalues en X = -1.
Pour déterminer a b et c, ya ptet plus académique mais jme rappele que de ca...
Tu peux tout multiplier par (X-1)^2 et évaluer en X = 1, tu détermines alors leq
Tu peux tout multiplier par (X-1) et faire tendre X vers l'infini tu obtiens alors
(avec d qu'on connait)
Et il faut une derniere pour avoir un systeme de trois eq a trois inconnues (a,b,c) on peut evaluer en un X quelconque (enfin, pas prendre un pole quand même) pis on DOIT avoir legalité. Donc en X=0 par exemple, on obtient
cqui devrait permettre de déterminer a, b et c
la vie est une fête 
merci de la réponse,
ouaou..!! je m'attendais pas à ça !!
ok pour partir de 1 / (p+1)(p-1)²
par contre en partant de la, la décomposition ne devrait pas etre :
A/(p+1) + (B/p-1) = C/(p-1)² ????
je pensais que la forme Ax+B/ () etais réservé a du polynome du secon degres??
et que les forme (p+1)^n donnait du:
Ax+B/ (x+1)^1 + Cx+D/(x+1)^1 + ......+A(n)x+B(n)/(x+1)^n
qu'est ce que j'ai mal compri ..
ouaou..!! je m'attendais pas à ça !!
ok pour partir de 1 / (p+1)(p-1)²
par contre en partant de la, la décomposition ne devrait pas etre :
A/(p+1) + (B/p-1) = C/(p-1)² ????
je pensais que la forme Ax+B/ () etais réservé a du polynome du secon degres??
et que les forme (p+1)^n donnait du:
Ax+B/ (x+1)^1 + Cx+D/(x+1)^1 + ......+A(n)x+B(n)/(x+1)^n
qu'est ce que j'ai mal compri ..
jtavouerai que ca remonte.
im semble que quand au dénominateur t'as un terme de premier degré (typiquement X-a), alors au numérateur tas un coeff simple.
Quand t'as un terme de second degré (X-a)^2 (ou X^2+bX+c) alors au numérateur t'as du aX+B, et si jamais tu as un truc du style (X-a)^5, jme rappele qu'on pose le changement de variable Y = X-a, mais apres j'ai oublié XD
Mais le plus sur ca reste de tenter cque j'ai proposé de faire. (genre evaluer pour plein de X et vérifier que la decomp est correcte) mais bon, là chu bien lancé pour faire un encéphalogramme plat :-)
im semble que quand au dénominateur t'as un terme de premier degré (typiquement X-a), alors au numérateur tas un coeff simple.
Quand t'as un terme de second degré (X-a)^2 (ou X^2+bX+c) alors au numérateur t'as du aX+B, et si jamais tu as un truc du style (X-a)^5, jme rappele qu'on pose le changement de variable Y = X-a, mais apres j'ai oublié XD
Mais le plus sur ca reste de tenter cque j'ai proposé de faire. (genre evaluer pour plein de X et vérifier que la decomp est correcte) mais bon, là chu bien lancé pour faire un encéphalogramme plat :-)
la vie est une fête 
Ce n'est pas tout à fait exact.
Lorsqu'on a un élément simple du type (X-a)^n, le numérateur est toujours constant. Par contre, lorsqu'on a un élément simple du type aX²+bX+c, ce qui n'est possible que si l'on travaille dans R (car dans C, tout polynôme est scincé), alors on aura un numérateur de la forme cX+d.
Lorsqu'on a un élément simple du type (X-a)^n, le numérateur est toujours constant. Par contre, lorsqu'on a un élément simple du type aX²+bX+c, ce qui n'est possible que si l'on travaille dans R (car dans C, tout polynôme est scincé), alors on aura un numérateur de la forme cX+d.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
