Soient
Je souhaite montrer que :
J'ai posé
Pour déterminer
Croissances comparées
3 messages
- Page 1 sur 1
Croissances comparées
par mehdi-128 » 17 Avr 2019, 12:45
Bonjour,
Soient >0)
on a : )^b}{x^a} = 0)
Je souhaite montrer que :
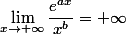
J'ai posé)
)^b}{x^a} = \lim\limits_{X \rightarrow +\infty} \dfrac{X^b}{e^{ax}} = 0)
Pour déterminer
je dois faire 1/0 donc la limite devrait être 
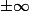
mais comment démontrer rigoureusement que c'est 
?
Soient
Je souhaite montrer que :
J'ai posé
Pour déterminer
Re: Croissances comparées
par Tuvasbien » 17 Avr 2019, 13:22
Tu travailles avec des quantités positives donc 
tend vers 
Re: Croissances comparées
par mehdi-128 » 17 Avr 2019, 15:29
Ah merci comme on est en + l'infini on peut prendre X >1 du coup toutes les quantité sont strictement positives
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :