Bonjour,
Dans le livre de Terence Tao, "Une Introduction à la Théorie de la Mesure", à l'exercice 1.2.7, il donne un critère de la Lebesgue mesurabilité qui est le suivant :

est mesurable si pour tout
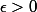
, il existe un ensemble Lebesgue mesurable

tel que
 \leq \epsilon)
.
Or, il me semble c'est étrange de définir la Lebesgue mesurabilité en faisant appel à une panoplie d'ensemble Lebesgue mesurables

. Quand j'ai posé la question sur un autre forum, on m'a répondu : "peut-être que l'auteur restreint son livre à des ensembles Lebesgue mesurables ?". Je n'ai pas trop su quoi répondre car Tao dit une phrase très vague (qui
pourrait laisser entendre qu'il restreint son étude à des ensembles Lebesgue mesurables), qui est la suivante : "Dans les pages qui vont suivre, nous allons établir les propriétés élémentaires de la mesure de Lebesgue. Grosso modo, ce concept possède toutes les propriétés qu'on pourrait demander intuitivement d'une mesure, ceci tant qu'on restreint notre attention à des opérations dénombrables et tant qu'on restreint notre attention à des ensembles Lebesgue mesurables."
Admettons que Tao ait restreint son livre à des ensembles Lebesgue mesurables, ce serait étrange d'introduire des critères pour la Lebesgue mesurabilité, quand tous les ensembles étudiés sont Lebesgue mesurables?
De plus, que se passerait-il si on ne se restreignait plus à des ensembles Lebesgue mesurables? Le critère cité plus haut ne serait plus valable ?
Enfin, un détail qui vient combler ma sidération est que, dans la preuve que le critère cité en début de question implique le critère "pour tout
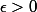
, il existe un ensemble ouvert

tel que
 \leq \epsilon)
", on n'utilise pas le fait que

soit mesurable.
En effet, on trouve un ouvert

contenant

et tel que la différence des mesures extérieures de Lebesgue de

et

ne dépasse pas epsilon. Ceci est possible, que

soit mesurable ou non.
Merci.
Très bonne journée.
