Courbe paramétrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Mar 2008, 20:46
par ptitmatteo » 07 Mar 2008, 20:46
bonjour,
voici mon sujet

1° je voudrais savoir car je sais comment on fait pour justifier la période mais je n'arrive pas a faire une simple addition
car
2sin(t)+sin(t).cos(2t)
et après je n'arrive pas a mettre sous forme d'une somme soit cos(t) + cos(r.t)
ou sin(t)+sin(r.t)
 par alavacommejetepousse » 07 Mar 2008, 20:51
par alavacommejetepousse » 07 Mar 2008, 20:51
bonsoir
pourquoi veux tu transformer l'expression pour la périodicité? inutile.
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Mar 2008, 22:05
par ptitmatteo » 07 Mar 2008, 22:05
bein enfaite je sais comment faire pour la periodicité mais pas dans une formule comme celle ci
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Mar 2008, 22:23
par ptitmatteo » 07 Mar 2008, 22:23
mais prendre la formule tel que je n'arrive pas a faire ma péridicité car je n'ai pas vue comme se si
??????
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 08 Mar 2008, 00:27
par ptitmatteo » 08 Mar 2008, 00:27
je pense avoir compris
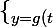=\cos t}^{x=f(t)=(2+\cos{2t})\sin t})
je dit que
}=\cos{(t+2\pi)}=\cos{(2t)})
}=\sin{(t+2\pi)}=\sin{(2t)})
et
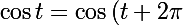}=\cos t)
mais je sais pas si c'est juste et je ne sais pas comment le rédigé
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 08 Mar 2008, 10:20
par ptitmatteo » 08 Mar 2008, 10:20
personne peut me dire si cela est juste?
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 08 Mar 2008, 14:38
par ptitmatteo » 08 Mar 2008, 14:38
vraiment personne?
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 08 Mar 2008, 22:18
par ptitmatteo » 08 Mar 2008, 22:18
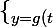=\cos t}^{x=f(t)=(2+\cos{2t})\sin t})
je dit que
}=\cos{2(t+2\pi)}=\cos{(2t)})
}=\sin{(t+2\pi)}=\sin{(2t)})
et
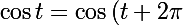}=\cos t)
je pense que cela est mieux
2°
=(2+\cos{-2t})\sin {-t}=-(2+\cos{2t})\sin t = -f(t))
et
=cos {-t}=cos t=g(t))
-mais après je ne sais pas comment trouver la symétrie
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Mar 2008, 09:17
par ptitmatteo » 09 Mar 2008, 09:17
je pense avoir compris
si mon raisonnement sur la parité de f(t) et g(t) alors je pense avoir trouvé la symétrie qui est une symétrie par rapport a l'axe des abscisse
????
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Mar 2008, 10:07
par ptitmatteo » 09 Mar 2008, 10:07
Mais es que je dois mettre des phrase particulière pour justifier ou rédigé
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Mar 2008, 13:17
par ptitmatteo » 09 Mar 2008, 13:17
oups dsl ........
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Mar 2008, 13:59
par ptitmatteo » 09 Mar 2008, 13:59
=cos t}^{f(t)=(2+cos {2t})sin t})
avec
=cos{(\pi-t)}}^{f(\pi-t)=(2+cos {(2(\pi-t)})sin {(\pi-t)}})
=- cos{t}}^{f(\pi-t)=(2-cos {(2t)})sin t})
mais la par contre je ne ou est la symétrie car f(t) na qu'une seule partie qui varie
????
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Mar 2008, 14:12
par ptitmatteo » 09 Mar 2008, 14:12
Personne peut m'aider a savoir pour la symétrie
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Mar 2008, 14:53
par ptitmatteo » 09 Mar 2008, 14:53
erreur?
=(2+cos{(2(\pi-t)})sin{(\pi-t)})
et
}=-cos {(2t)})
et
}=sin t)
donc je ne vois ou est l'erreur????
 par alavacommejetepousse » 09 Mar 2008, 14:58
par alavacommejetepousse » 09 Mar 2008, 14:58
ptitmatteo a écrit:erreur?
}=-cos {(2t)})
donc je ne vois ou est l'erreur????
exactement là
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Mar 2008, 15:09
par ptitmatteo » 09 Mar 2008, 15:09
AH OUI
c'est vrais je n'avais pas vus le 2

donc
=(2+cos{(2\pi-2t))}sin{(\pi-t)})
=(2+cos{(2t)}sin t=f(t))
donc on a:
=-g(t)}^{f(\pi-t)=f(t)})
alors je pense qu'il y a une symétrie par rapport a l'axe des abscisse
es mieux???
mais si cela est juste alors ma première symétrique est fausse car elle n'est pas par rapport a l'axe des abscisse mais des ordonné
????
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités

