Coordonnées cartesiennes/barycentriques
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Fév 2007, 18:38
par barbu23 » 18 Fév 2007, 18:38
Bonjour:
Dans le cours, il y'a le passage suivant:
Etant donné un espace affine

de dimension finie et

sa direction, on se donne
$)
une base de

, et

un point de

. Alors tout point

de

s'écrit de manière unique sous la forme

)
Avec

défini par

, la famille
 $)
est appelée repère affine de

; c'est en particulier une famille affinement libre. Il est suffisant pour qu'une famille affinement libre soit un repère affine que son cardinal soit
 $)
.
 $)
est appelé repère cartésien de

.
Les

sont appelés coordonnées cartésiennes de

.
On note qu'avec

, la relation
)
équivaut à la relation

)
Pourriez vous m'indiquer comment on etablit cette implication ( c'est à dire :
 \Rightarrow (*) $)
) au moyen des expressions de la forme par exemple:
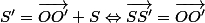
( passage de points au vecteurs ) surtout que je ne sais pas d'ou sort le terme

dans la relation
 $)
avec biensûr:

.
et merçi d'avance !!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Fév 2007, 18:48
par fahr451 » 18 Fév 2007, 18:48
bonsoir
par définition
ei = oxi (tout en vecteur)
et ox = sigma ti oxi
et oo = vecteur nul
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Fév 2007, 19:39
par barbu23 » 18 Fév 2007, 19:39
Bonsoir fahr451 :
je suis d'accord avec toi pour la remarque que tu viens de donner, neanmoins, le problème pour moi c'est que je ne comprends pas d'ou vient le terme

dans l'expression :

)
.
Dans la suite du cours l'auteur donne une expression generale du point barycentrique :
avec

, si bien que pour tout

:

On a (dans ce cas, c'est-à-dire avec les

formant une base de

) existence et unicité de cette décomposition barycentrique.
Les

tels que

et
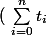 \vec {Mx} = t_0. \vec{MO} + t_1. \vec {Mx_1} + ... + t_n. \vec {Mx_n} $)
sont appelés des coordonées barycentriques de

dans le repère affine
 $)
.
Les

tels que

et

sont appelés les coordonées barycentriques normalisées de dans le repère affine
 $)
. .
Est ce que tu peux me dire aussi comment on aboutit au fait que :
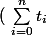 \vec {Mx} = t_0. \vec{MO} + t_1. \vec {Mx_1} + ... + t_n. \vec {Mx_n} $)
au moyen des calculs avec

.
et merçi infiniment !!!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Fév 2007, 20:14
par fahr451 » 18 Fév 2007, 20:14
en fait
tu réponds toi même
il introduit ce t0 pour avoir une somme qui vaut 1
il a la relation d 'abord pour M = 0
ensuite elle est vraie pour tout M
Mx = MO +Ox = 1M0+ toOO +...+tnOxn = (t0+...+tn)MO+t0OO +...+tn0xn =
t0M0 +...+ tnMxn
et quand la somme n 'est pas égale à 1 il suffit de diviser par la somme pour se ramener au cas précédent
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Fév 2007, 20:47
par barbu23 » 18 Fév 2007, 20:47
resalut:
et ben c'est trouvé..!! tout decoule de la definition du barycentre:

est le barycentre de l'ensemble des points
)
si et seulement si

avec
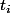
le poinds relatif à chaque

pour

.
après devellopement :
 \vec {xM} + \sum_{i=0}${n} t_i. \vec {Mx_i} + t_0. \vec {OM} = 0<br />\Longleftrightarrow <br />(\sum_{i=0}${n} t_i) \vec {Mx} = t_0. \vec {MO} + \sum_{i=1}${n} t_i. \vec {Mx_i} = t_0. \vec {MO} + t_1. \vec {Mx_1} +...+ t_n. \vec {Mx_n})
d'ou le resultat general.
ensuite pour

et

on obtient :

d'où le resultat !!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
de dimension finie et
sa direction, on se donne
une base de
, et
un point de
. Alors tout point
de
s'écrit de manière unique sous la forme

défini par
, la famille
est appelée repère affine de
; c'est en particulier une famille affinement libre. Il est suffisant pour qu'une famille affinement libre soit un repère affine que son cardinal soit
.
est appelé repère cartésien de
.
sont appelés coordonnées cartésiennes de
.
, la relation
équivaut à la relation

