Ln-Convexité de Gamma

[Alpha]

Bonjour,

Je voulais savoir si vous pouviez me fournir une ou plusieurs démonstrations de la ln-convexité de la fonction Gamma d'Euler.

Je rappelle l'expression de la fonction Gamma :
, définie pour
Merci d'avance.

Alpha

[Mikou]

Un fonction deux fois derivable est convexe si et seulement si f'' >0 ( ou s'annule eventuellement en qq pts isolés )

[mathelot]

bonjour,

Dans "calcul infinitésimal" de Dieudonné, on trouve la
formule de Weierstrass:
pour tout z complexe distinct des points -n ()
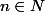
cette formule restreinte à indique immédiatement que la dérivée de est strictement croissante.

cordialement.

[Alpha]

Merci beaucoup! J'ai déjà dû voir la formule dont tu parles, même si je ne l'ai jamais démontrée. Je vais regarder ça attentivement. :lol4:

[Alpha]

J'avoue avoir du mal à retrouver la formule de Weierstrass... Quelqu'un saurait-il la montrer, ou montrer la convexité de ln(gamma) par une autre méthode?

Merci.

[Alpha]

Personnellement, je ne vois toujours pas comment montrer la formule de mathelot.

Pour montrer la convexité de ln(gamma), au début, j'avais dérivé ln(gamma) deux fois, sachant que la dérivée seconde de ln(f) est du signe de f"f - f'², j'avais pensé à combiner du Cauchy-Schwarz et de l'intégration par parties... Ca n'avait pas bien fonctionné... Cette voie peut-elle cependant aboutir?

Merci

[mathelot]

les étapes de Dieudonné (calcul infinitésimal),on pose:
pour
en intégrant par parties:

par symétrie:

par récurrence:

or:
pour x>0


introduire le prolongement analytique et passer au log pour la formule de Weierstrass.
en fait, ce sont des pages à détailler. Le mieux,c 'est de consulter le livre.

[Alpha]

Merci beaucoup, je regarde tout ça et je reviendrai pour te dire si j'ai tout compris.

:lol4: