Bonsoir.
[INDENT]Voici la définition du coefficient de convergence d'une suite
_n)
de nombres réels ayant pour limite
. On suppose que
. On considère la suite
_n=(\frac{u_{n+1}-l}{u_n-l})_n)
(noté aussi
)
lorsqu'il y a ambiguïté). Si cette suite converge vers une limite réelle
, alors
est dit coefficient de convergence de la suite
(noté également
lorsque risque d'ambiguïté). On démontre que, lorsqu'il existe, on a
.[/INDENT]
Premier bug : le prof écrit que le fait que
ne signifie pas "non stationnaire". Que dois-je comprendre ? Pour une suite stationnaire, le coefficient de convergence est bien défini et vaut 0 ?
[INDENT]Soient
et
_n)
deux suites convergentes vers
telles que
. On dit que la convergence de la suite
vers
est plus rapide que celle de
si
.
[/INDENT]
Deuxième bug : pourquoi faut-il avoir la condition
? Ne peut-on pas se contenter de
?
[INDENT]Enfin, une proposition qui me perturbe sur certains points.[/INDENT]
[CENTER]Si
alors
converge plus vite que
[/CENTER]
Preuve : (italique : mes commentaires)
On pose
. Alors on a
}{\lambda_n(v)}x_n)
.
Pour pouvoir considérer une telle écriture, il faut supposer que . Mais était-ce nécessaire de l'inclure dans la définition de rapidité de convergence ?Alors on a
}{\lambda_n(v)})
.
Ici encore, on s'aperçoit qu'on ne peut pas écrire cela sans la condition .On fixe k telle que
et alors il existe
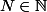
telle que
}{\lambda_n(v)}\le k)
.
Ici, je suis perdu 
Totalement.Par conséquent, on a
.
Il va un peu vite, mais pour moi }{\lambda_n(v)}||x_n|)
et }{\lambda_n(v)}|)
et }{\lambda_n(v)})
c'est quand même différent !On en déduit par récurrence que
et donc le résultat par passage à la limite sur p.
Ok pour la fin.
Merci pour toutes aides !
:id:
