Comportement à l'infini

[Babe]

Bonjour,

j'ai un peu de mal à saisir cet enoncé

"resoudre l'equa diff u'=e^t -u et etudiez suivant la condition initiale u(0) le comportement des solutions à l'infini"

j'ai resolu l'equa diff et je trouve u=e^-t + (1/2)e^(2t) + Cste
je ne comprends pas la deuxieme partie de la question

merci

[nuage]

Salut,
si ton équation est bien :

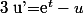
je ne suis pas d'accord avec tes solutions.

Pour le comportement à l'infini on donne la limite en plus l'infini et en moins l'infini (éventuellement un équivalent).

[Babe]

solution homogène
u'+u=0
u'=-u
u'/u=-1
u=Ke^-t avec K=cste

variation de la constante
K'(t)e^-t - K(t)e^-t + K(t)e^-t =e^t
K'(t)e^-t=e^t
K'(t)=e^(2t)
d'où K(t)=(1/2)e^(2t) + cst
donc u=((1/2)e^2t + cst)e^-t

solution general:u=e^-t + ( (1/2)e^(2t) + C)e^-t

c'est bon ?

[nuage]

C'est bon.
on peut aussi écrire
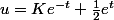
étant une constante ()

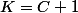
[Babe]

etudiez suivant la condition initiale u(0) le comportement des solutions à l'infini

je dois regarder quand u->oo et u->-oo ?
je comprends pas le "u(0)" si je remplace t par 0 je ne peux pas etudier les limites infini

[nuage]

La valeur de u(0) te donne celle de la constante. Ce qui permet d'étudier la limite en moins l'infini. Pour la limite en plus l'infini il n'y a pas de problème avec la constante.

[Babe]

C'est bon.
on peut aussi écrire
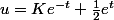
étant une constante ()

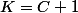
u(0)=K+(1/2)
je ne vois pas en quoi cela m'aide

t->oo, u->oo ?
t->-oo, u->oo si K>0 ?
est ce le raisonement qu'il demande ?

[nuage]

u(0)=K+(1/2)
je ne vois pas en quoi cela m'aide

t->oo, u->oo ?
t->-oo, u->oo si K>0 ?
est ce le raisonement qu'il demande ?

Il manque quelques signes + et - mais c'est l'idée.
On a 3 cas à distinguer :
K>0
K=0
K<0

[Babe]

t->oo, u->oo
t->-oo, u->oo si K>0
t->-oo, u->-oo si K<0
pour K=0 j'ai une forme indeterminé

[alben]

Bonjour,
Moi, j'aurais plutôt écrit puisqu'on nous parle de conditions initiales.
Soit encore .
Pour t->+oo , il en sera de même de u.
Si t->-oo, cela dépendra si u(0) <0,5 ou pas (mais il n'y a rien d'indéterminé)