Classe infini

[jonses]

Bonjour ou bonsoir,

J'ai un petit cherché (sur le forum, et ailleurs) pour savoir comment montrer qu'une fonction est de classe infini, mais je n'ai pas très bien saisi ce que j'ai lu :

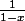
par exemple si je veux montrer que la fonction f qui à tout réel x différent de 1 associe est de classe infini, est-ce qu'il faut que je fasse une récurrence sur n pour montrer que la n-ème dérivée de cette fonction est dérivable (et donc continue),c'est-à-dire montrer que : est dérivable ?

Merci d'avance pour vos réponses

[mrif]

Cela dépend de l'expression de la fonction.

Par exemple une fonction polynome est C infini car la dérivée d'un polynome est un polynome.

La fonction de ton exemple est C infini sur son domaine de définition car c'est une fraction rationnelle qu'on peut ecrire (1-x)^(-1) qu'on peut dériver indéfiniment sur son domaine de définition.

[jonses]

Cela dépend de l'expression de la fonction.

Par exemple une fonction polynome est C infini car la dérivée d'un polynome est un polynome.

La fonction de ton exemple est C infini sur son domaine de définition car c'est une fraction rationnelle qu'on peut ecrire (1-x)^(-1) qu'on peut dériver indéfiniment sur son domaine de définition.

Je suis d'accord, mais je suis sur un exercice où justement je dois montrer cela, et je ne sais pas si je peux raisonner par récurrence comme je l'ai écrit plus haut pour montrer qu'elle est de classe infini

[Ben314]

Salut,
De toute façon, à un moment ou un autre il faut faire une (vague) récurrence : quand mrif écrit "une fonction polynome est C infini car la dérivée d'un polynome est un polynome." en fait, c'est une récurrence, mais tellement évidente qu'en général on l'écrit pas.

Idem pour les fractions rationnelles où il faut normalement faire une récurrence qui utilise uniquement le fait que la dérivée d'une fraction rationnelle est une fraction rationnelle de même ensemble de définition.

Concernant ton exo, si tu veut uniquement montrer qu'elle est C^oo, ça te coute pas un kopeck de plus de montrer que toutes les fraction rationnelles sont C^oo (c'est exactement la même preuve...)
Par contre, dans le cas de ton exo, on peut en plus avoir la formule exacte de la dérivée n-ième de f, donc ça risque de valoir le coup de tout montrer en même temps avec une seule récurrence (qu'elle est de classe C^n ET que sa dérivée n-ième est blablabla)

[jonses]

Concernant ton exo, si tu veut uniquement montrer qu'elle est C^oo, ça te coute pas un kopeck de plus de montrer que toutes les fraction rationnelles sont C^oo (c'est exactement la même preuve...)
Par contre, dans le cas de ton exo, on peut en plus avoir la formule exacte de la dérivée n-ième de f, donc ça risque de valoir le coup de tout montrer en même temps avec une seule récurrence (qu'elle est de classe C^n ET que sa dérivée n-ième est blablabla)

C'est ce que je voulais faire (faire une récurrence pour montrer que la n-ème dérivée est dérivable, de dériver blabla), mais je savais pas si dans la récurrence je dois écrire "la n-ème dérivée est dérivable de dérivée blabla", ou "la n-ème dérivée est de classe C^n et dé dérivée blabla", mais en lisant ce que tu me dis, je pense que j'ai compris, et qu'en fait c'est aucun des deux et que c'est "la fonction en question est de classe C^n, etc"

Merci beaucoup !