Carré de la norme non lipschitzienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
allmess
- Membre Naturel
- Messages: 70
- Enregistré le: 12 Sep 2014, 18:46
-
 par allmess » 15 Mar 2016, 19:28
par allmess » 15 Mar 2016, 19:28
Bonjour,
je n'arrive pas à montrer que
=|| x||^2$)
qui applique de

n'est pas lipschitzienne, mais qu'elle l'est sur un ensemble borné.. A vrai dire c'est le premier exercice que j'aborde dans ce genre et je n'ai donc pas dutout la technique..
Merci d'avance!
-
allmess
- Membre Naturel
- Messages: 70
- Enregistré le: 12 Sep 2014, 18:46
-
 par allmess » 15 Mar 2016, 19:54
par allmess » 15 Mar 2016, 19:54
Par exemple, est ce que ce qui suit est correcte?
On prend
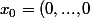)
et

; alors

, d'où f n'est pas lipschitzienne...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 15 Mar 2016, 19:58
par Doraki » 15 Mar 2016, 19:58
Euh tu veux dire quoi par "tend vers l'infini" ?
Sinon oui c'est à peu près ça.
-
allmess
- Membre Naturel
- Messages: 70
- Enregistré le: 12 Sep 2014, 18:46
-
 par allmess » 15 Mar 2016, 20:02
par allmess » 15 Mar 2016, 20:02
Merci beaucoup pour ta réponse!
Pour x qui tend vers l'infini, IIxII tend vers l'infini.. Si ça a un sens de dire que x tend vers l'infini...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 15 Mar 2016, 20:33
par Doraki » 15 Mar 2016, 20:33
Certes, lorsque ||x|| tend vers l'infini, ||x|| tend vers l'infini aussi.
Pour montrer qu'une fonction n'est pas lipschitzienne, il faut montrer qu'elle n'est pas k-lipschitzienne pour aucun k> 0.
Le mieux c'est de sortir directement un contre-exemple pour chaque k,
donc dans ton cas il suffit de sortir (pour chaque k) un y dont la norme est > k, comme ça tu auras |f(x0)-f(y)| / ||x0-y|| = ||y||²/||y|| = ||y|| > k, et donc f ne peut pas être k-lipschitzienne.
-
allmess
- Membre Naturel
- Messages: 70
- Enregistré le: 12 Sep 2014, 18:46
-
 par allmess » 15 Mar 2016, 20:37
par allmess » 15 Mar 2016, 20:37
Merci!
mais alors comment faire si l'on se place sur un ensemble borné? Car alors llxll<N avec N donné... Mais cela suffit il?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 15 Mar 2016, 20:57
par Doraki » 15 Mar 2016, 20:57
Ben non, il faut que tu montres que pour tout N, il existe une contante mystérieuse K(N) telle que pour tout x,y, si ||x||, ||y|| <= N alors |f(x)-f(y)| <= K(N) * ||x-y|| (c'est à dire | ||x||²-||y||² | <= K(N) * ||x-y||.
Là vu la tête de la fonction ça serait pas idiot de faire ça en deux étapes,
et de montrer qu'il existe des constantes K1 K2 (qui dépendent de N),
telles que si ||x||, ||y|| <= N alors | ||x||²-||y||² | <= K1 * | ||x||-||y|| | et | ||x||-||y|| | <= K2 * ||x-y||.
-
allmess
- Membre Naturel
- Messages: 70
- Enregistré le: 12 Sep 2014, 18:46
-
 par allmess » 16 Mar 2016, 19:22
par allmess » 16 Mar 2016, 19:22
Super, merci,
Alors: L'ensemble étant borné, il existe M tel que pour tout x, y de l'ensemble, IIxll,llyll<=M
On a
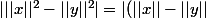(||x||+||y||)|)
. Or
 \leq 2M)
, aussi

. Et on démontre facilement que

. D'où le résultat..
Un grand merci pour ton aide!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités