http://www.noelshack.com/2015-11-1426009329-sujet-capes.png
Jai un capes blanc a faire. J'ai, je pense, reussi les question 1)a et 1)b, mais je ne sais absolument pas comment trouver la matrice U
Et comme tout le reste dépend de ca...
Dans l'enoncé U* est la transposé de U
Vous seriez vraiment très aimable de me donner un coup de main. Merci beaucoup
Capes blanc matrice
2 messages
- Page 1 sur 1
Bonsoir ! Il me semble que ce problème concerne C et non R, donc U* n'est pas la transposée mais l'adjoint (d'ailleurs c'est la bonne notation).
Pour la question 3, j'ai calculé dét) : en écrivant le déterminant, on voit qu'on peut le développer à partir du
: en écrivant le déterminant, on voit qu'on peut le développer à partir du  en haut à gauche et du 1 en bas à droite, ce qui donne
en haut à gauche et du 1 en bas à droite, ce qui donne ^{n-1} D_2) où
où  est un déterminant diagonal, donc égal au produit de ses n-1 éléments diagonaux qui sont les
est un déterminant diagonal, donc égal au produit de ses n-1 éléments diagonaux qui sont les  , et
, et 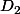 est aussi un déterminant diagonal dont les n-1 éléments diagonaux sont des 1. Bref, si je ne me trompe pas ça donne :
est aussi un déterminant diagonal dont les n-1 éléments diagonaux sont des 1. Bref, si je ne me trompe pas ça donne :
dét = (-1)^n\left( \lambda^n - 1 \right)) .
.
(J'ai vérifié rapidement avec n=3 et n=4.)
Dans C, ce polynôme admet n racines : les racines n-èmes de 1, c'est-à-dire les) où k varie de 0 à n-1.
où k varie de 0 à n-1.
Reste ensuite à calculer les sous-espaces propres : s'ils sont chacun de dimension 1, la matrice sera diagonalisable (dans C).
Pour la valeur propre 1, par exemple, c'est très simple : w(u) = u ssi (en utilisant la matrice)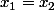 ,
,  , et ainsi de suite jusque
, et ainsi de suite jusque  , par conséquent le sous-espace propre est la droite engendrée par (1, 1, ... , 1). (Il était d'ailleurs évident que ce vecteur est vecteur propre puisque, d'après la première question, w échange les vecteurs de base.)
, par conséquent le sous-espace propre est la droite engendrée par (1, 1, ... , 1). (Il était d'ailleurs évident que ce vecteur est vecteur propre puisque, d'après la première question, w échange les vecteurs de base.)
La matrice U sera la matrice de passage, donc la matrice dont les colonnes sont les coordonnées de vecteurs propres.
Pour la question 3, j'ai calculé dét
dét
(J'ai vérifié rapidement avec n=3 et n=4.)
Dans C, ce polynôme admet n racines : les racines n-èmes de 1, c'est-à-dire les
Reste ensuite à calculer les sous-espaces propres : s'ils sont chacun de dimension 1, la matrice sera diagonalisable (dans C).
Pour la valeur propre 1, par exemple, c'est très simple : w(u) = u ssi (en utilisant la matrice)
La matrice U sera la matrice de passage, donc la matrice dont les colonnes sont les coordonnées de vecteurs propres.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
