En fait, en réfléchissant un peu (des fois ça sert...), il me semble qu'une fois l'ordre fixé, il n'y a pas 36000 façons de décomposer une rotation (vectorielle)

en composée de rotations suivant les axes :
Si on part par exemple sur du

avec

des rotations suivant les axes, ça signifie que

doit être une rotation suivant l'axe des

et comme une composée de rotations (vectorielles) est toujours une rotation, il suffit de vérifier que l'axe de cette composée est bien l'axe des

, c'est à dire que le vecteur
)
est invariant.
Et si on pose
=R(e_1))
(qui est la 1er colonne de la matrice de

), ce qu'on veut, c'est que
=R_y(e_1))
. Or, en faisant varier l'angle, les
)
décrivent tout les vecteurs (de norme 1) du plan vectoriel

donc il faut chercher l'angle

de
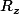
de façon à ce que
=(?,0,?))
c'est à dire
a\!+\!\cos(\gamma)b\!=\!0)
ce qui permet de déterminer

modulo

(donc deux solutions modulo

) sauf dans le cas particulier où
=(\pm 1,0,0)=\pm e_1)
où on peut prendre n'importe quoi comme angle.
Et une fois l'angle de
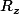
choisi (parmi les deux solutions sauf exception), il me semble qu'il n'y aura plus le choix pour les autres angles.
BILAN : Il y a toujours exactement deux décomposition possibles, sauf lorsque
=\pm e_1)
où il y a une infinité de solutions.
EDIT : Pour pas mourir idiot (et en attendant que Neivalf décrive clairement son problème), je suis allé chercher sur le net cette histoire de décomposition en rotations d'axes les axes du repère : il y a effectivement un truc classique utilisé semble-t-il en mécanique : les "angles d'Euler", mais ça colle moyen vu que c'est une décomposition style

avec deux fois l'axe des

...
 ).
).
