Calcul d'une derivée

[Rik95]

Bonsoir,

J'aurai besoin de votre aide pour le calcul d'une dérivée :

(x(2-7x)^1/2)^-1/5

Voici ce que j'ai trouvé en essayant mais je ne suis pas sur du résultat :
(-1/5)x^((-1/5) -1).(2-7x)^-1/10 + (x^-1/5).(-1/10).(2-7x)^((-1/10) -1).(-7)

Désolé pour cette longue expression mais je n'ai pas su simplifier :(

J'aurai egalement besoin d'une confirmation pour une autre dérivée :

(1 +1/x) ^x

Voici ce que j'ai trouvé :

(ln(1+1/x) -1/(x+1) ).e^xln(1+1/x)

Merci

[zaidoun]

Je confirme pour la deuxième dérivée.

[BiancoAngelo]

Bonsoir,

J'aurai besoin de votre aide pour le calcul d'une dérivée :

(x(2-7x)^1/2)^-1/5

Voici ce que j'ai trouvé en essayant mais je ne suis pas sur du résultat :
(-1/5)x^((-1/5) -1).(2-7x)^-1/10 + (x^-1/5).(-1/10).(2-7x)^((-1/10) -1).(-7)

Désolé pour cette longue expression mais je n'ai pas su simplifier

J'aurai egalement besoin d'une confirmation pour une autre dérivée :

(1 +1/x) ^x

Voici ce que j'ai trouvé :

(ln(1+1/x) -1/(x+1) ).e^xln(1+1/x)

Merci

La première, ça donne : .
Donc on a :

Donc

Et c'est bien ce que tu as écrit.

[Rik95]

Nickel Merci :)

Je profite de ce post pour poser une question par la même occasion, quand on dis qu'une fonction est définie et continue sur un intervalle [a, b] , est ce qu'on dois toujours dire qu'elle est dérivable sur l'intervalle ]a, b[ ouvert puis étudier la dérivabilités en ces points ?

[BiancoAngelo]

Nickel Merci

Je profite de ce post pour poser une question par la même occasion, quand on dis qu'une fonction est définie et continue sur un intervalle [a, b] , est ce qu'on dois toujours dire qu'elle est dérivable sur l'intervalle ]a, b[ ouvert puis étudier la dérivabilités en ces points ?

Non, pas du tout. La continuité n'implique pas la dérivabilité.
Tu dois étudier tout l'intervalle correctement.

Tu veux un exemple, affiche sur ta calculatrice la fonction par exemple, c'est continu mais...

[Rik95]

Mmmm ok, pourrai tu m'expliquer rapidement la marche a suivre stp ?

car par exemple quand je vois une fonction qui n'est pas définie en 0 je sais que je dois etudier la derivabilité en ce point seulement mais comment je montre que c'est bon pour tout les autres points ?

par exemple si je prend la fonction x²cos1/x , il n'y a que la dérivabilité en 0 qui pose probleme mais comment je fais pour montrer que c'est bon pour tout les autres points ?

[BiancoAngelo]

Mmmm ok, pourrai tu m'expliquer rapidement la marche a suivre stp ?

car par exemple quand je vois une fonction qui n'est pas définie en 0 je sais que je dois etudier la derivabilité en ce point seulement mais comment je montre que c'est bon pour tout les autres points ?

par exemple si je prend la fonction x²cos1/x , il n'y a que la dérivabilité en 0 qui pose probleme mais comment je fais pour montrer que c'est bon pour tout les autres points ?

En annonçant que si , ce sont des fonctions (produit, composée...) sur un domaine où elles sont dérivables... partout... partout... partout sauf en 0...

[Rik95]

Ok merci :)

[Rik95]

Desolé du double poste mais j'aurai besoin d'un autre resultat concernant une limite svp :

Lim (f(x)e^x -f(a))/(f(x)cosx - f(a)) quand x tend vers 0 avec a = 0 et f'(0) différent de 0.

Perso j'ai trouvé ceci : (f'(0) + f(0))/f'(0)

Et aussi que puis je dire a propos de la dérivabilité de cette fonction : x*abs(x)

Elle est dérivable sur tout R non ? il n'y a aucun point a étudier ? ( l'exo dit d’étudier la dérivabilité )

Et pour la fonction : log(indice x ) cosx avec x appartenant a ] 0 pi/2 [ sauf 1

Dans ce dernier cas, je dois étudier la dérivabilité en 0 et pi/2 ?

[BiancoAngelo]

Desolé du double poste mais j'aurai besoin d'un autre resultat concernant une limite svp :

Lim (f(x)e^x -f(a))/(f(x)cosx - f(a)) quand x tend vers 0 avec a = 0 et f'(0) différent de 0.

Perso j'ai trouvé ceci : (f'(0) + f(0))/f'(0)

Et aussi que puis je dire a propos de la dérivabilité de cette fonction : x*abs(x)

Elle est dérivable sur tout R non ? il n'y a aucun point a étudier ? ( l'exo dit d’étudier la dérivabilité )

Et pour la fonction : log(indice x ) cosx avec x appartenant a ] 0 pi/2 [ sauf 1

Dans ce dernier cas, je dois étudier la dérivabilité en 0 et pi/2 ?

Bonjour,

1)



Etrange, il n'y a pas une erreur d'énoncé ?

2)
n'est pas dérivable en 0... Donc tu dois bien étudier en 0, (le reste c'est ok, vu que c'est dérivable). As-tu au moins regardé la fonction que je t'ai mise hier, on voit bien toutes les "pointes" de la fonction qui la rendent non dérivable...

3) Dans le dernier cas, pense que ta fonction s'écrit
Etudie les limites aux bornes, vois d'abord si c'est continu, et après regarde la dérivabilité (là où c'est continu).

[Ben314]

Salut,
Si on suppose dérivable en 0, alors on a :

si

@BiancoAngelo : dans une limite, soit on "remplace" tout les x par la valeur limite (si les fonction sont continues), soit aucun d'entre eux, mais on ne remplace jamais la moitié d'entre eux par la valeur limite.
Par exemple, dans , si tu ne remplace que le x du f(x) par 0, ça simplifie grandement le calcul, mais... ça te donne pas vraiment le bon résultat...

[Ben314]

Salut,
Si on suppose dérivable en 0, alors on a :

si

@BiancoAngelo : dans une limite, soit on "remplace" tout les x par la valeur limite (si les fonction sont continues), soit aucun d'entre eux, mais on ne remplace jamais la moitié d'entre eux par la valeur limite.
Par exemple, dans , si tu ne remplace que le x du f(x) par 0, ça simplifie grandement le calcul, mais... ça te donne pas vraiment le bon résultat...

[Rik95]

Merci pour vos réponses, pour la fonction abs(x) je ne comprend pas pourquoi n'est elle pas dérivable en 0 ?
J'ai essayer de voir la fonctions sin(abs(x)) en graph mais comment peu tu savoir si elle est dérivable ou non a partir de sa ?

[BiancoAngelo]

Salut,
Si on suppose dérivable en 0, alors on a :

si

@BiancoAngelo : dans une limite, soit on "remplace" tout les x par la valeur limite (si les fonction sont continues), soit aucun d'entre eux, mais on ne remplace jamais la moitié d'entre eux par la valeur limite.
Par exemple, dans , si tu ne remplace que le x du f(x) par 0, ça simplifie grandement le calcul, mais... ça te donne pas vraiment le bon résultat...

Oui merci Ben, je ne sais même pas pourquoi j'ai écrit ça... :mur: J'étais pas dans mon état normal... lol

[BiancoAngelo]

Merci pour vos réponses, pour la fonction abs(x) je ne comprend pas pourquoi n'est elle pas dérivable en 0 ?
J'ai essayer de voir la fonctions sin(abs(x)) en graph mais comment peu tu savoir si elle est dérivable ou non a partir de sa ?

Si tu étudies la limite du taux d'accroissement de f en 0 quand x tend vers 0, tu vois que la limite est différente à gauche et à droite.

Ca veut dire qu'on peut seulement tracer deux demi-tangentes en 0.

Globalement, être dérivable, c'est ne pas être "pointu"... style valeur absolue.

[BiancoAngelo]

@ Ben :

On peut remplacer seulement certains par leurs valeurs dans une limite seulement s'il n'y a pas de somme, non ?
Vu qu'en fait l'équivalence ~ n'est pas compatible avec la somme, c'est ça ?

EDIT: en fait, on a le droit de le faire seulement quand ce n'est pas une forme indéterminée, du style 0/0 que tu m'as donné en exemple... + qu'il n'y ait pas de somme et de composées...

Est-ce que c'est ça au final ?

Parce que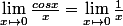
Mais ...

Donc en fait l'erreur vient du fait qu'on est tenté d'assimiler la notion de limite à celle d'équivalence alors que c'est clairement faux en 0...

Est-ce que c'est ça ?

D'ailleurs, vue la définition de l'équivalence, si f ~*0 en a, c'est que f est la fonction nulle au voisinage de a ? Donc si a est un nombre réel (-> non infini), la fonction doit faire 0 sur tout un voisinage, et pas seulement approcher 0.

Tu peux confirmer/infirmer mes propos ?

[Rik95]

je vois ce que tu veux dire, enfaite c'es evident pour x > 0 on a abs x = x
pour x < 0 on a abs x = -x et pour x = 0 des 2 cotés on a x = 0

[BiancoAngelo]

je vois ce que tu veux dire, enfaite c'es evident pour x > 0 on a abs x = x
pour x < 0 on a abs x = -x et pour x = 0 des 2 cotés on a x = 0

Oui, en fait, et

Donc la limite du taux d'accroissement de la valeur absolue en 0 n'existe pas quand x tend vers 0.

[Rik95]

Dacc donc par exemple pour la fonction suivante : (abs(x)*racine(x²-2x+1))/(x-1)

Je devrai etudier la derivabilité en x = 1 et en x = 0 a cause la valeur absolue de x ?

Edit : Ici en l’étudiant de cette façon j'ai trouvé qu'elle n’était pas dérivable en 0 car d'un coté la limite est egal a 1 et de l'autre -1 mais elle est dérivable en 1 car la limite des 2 cotés est égal a 0

[BiancoAngelo]

Dacc donc par exemple pour la fonction suivante : (abs(x)*racine(x²-2x+1))/(x-1)

Je devrai etudier la derivabilité en x = 1 et en x = 0 a cause la valeur absolue de x ?

En x= 0, c'est sûr, à cause de la valeur absolue.

Puis, si c'est continu en x = 1, oui, car racine n'est pas dérivable en 0, même si ici, ce ne sont que des valeurs absolues ...