Calcul de limite: (tan(3x/2))^tan(3x)
15 messages
- Page 1 sur 1
Calcul de limite: (tan(3x/2))^tan(3x)
Bonjour a tous, je suis nouveau sur le forum, je suis actuellement dans le passage de ma première année de prépa TSI à ma seconde année ( les concours arrivent vite ! ) et j'ai beaucoup d'exos a faire pendant les vacs, je voudrais vous en montrer un pour que vous puissiez me dire ce que vous en pensez. ( J'ai cherché évidemment par moi même avant ).
Déterminer lim quand x tend vers PI/6 de la fonction f(x)= (tan(3x/2))^tan(3x) ( le tan(3x) est bel et bien en exposant )
Pour se faire j'ai commencé par étudier la fonction f((PI/6)+h) quand h tend vers 0. ( x=(PI/6)+h) )
Donc on obtient : (tan((PI/4)+(3h/2))^tan((PI/2)+3h)
Avec les formules tan=sin/cos et sin(a+b)=sin(a)cos(b)+sin(b)cos(a) et cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
J'obtient que mon tangente qui était en exposant vaut au final : -1/tan(3h)
Je fais pareil pour l'autre.
Qu'en pensez vous ? est-ce que je démarre bien ?
J'ai trouver une limite mais je ne suis pas sur ...
Déterminer lim quand x tend vers PI/6 de la fonction f(x)= (tan(3x/2))^tan(3x) ( le tan(3x) est bel et bien en exposant )
Pour se faire j'ai commencé par étudier la fonction f((PI/6)+h) quand h tend vers 0. ( x=(PI/6)+h) )
Donc on obtient : (tan((PI/4)+(3h/2))^tan((PI/2)+3h)
Avec les formules tan=sin/cos et sin(a+b)=sin(a)cos(b)+sin(b)cos(a) et cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
J'obtient que mon tangente qui était en exposant vaut au final : -1/tan(3h)
Je fais pareil pour l'autre.
Qu'en pensez vous ? est-ce que je démarre bien ?
J'ai trouver une limite mais je ne suis pas sur ...
Bonjour à tous.
Je vous propose de calculer^{g(x)}) dans le cas où celle-ci est la forme indéterminée
dans le cas où celle-ci est la forme indéterminée 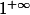 .
.
On a donc=1) et
et =+\infty)
On essaie de calculer^{g(x)})) et si celle-ci existe, disons
et si celle-ci existe, disons 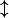 , alors
, alors ^{g(x)}=e^{\mathcal{l} }) .
.
Comme=1) et comme
et comme =1+(f(x)-1)= 1+h(x)) ,
, =f(x)-1 \to 0) quand
quand 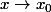 ,
,
on peut alors écrire)\sim h(x)=f(x)-1) et
et  \ln(f(x)) \sim g(x)(f(x)-1)) , on en déduit que si
, on en déduit que si
(f(x)-1)) existe, alors
existe, alors ^{g(x)}=e^{\lim_{x \to x_0} g(x)(f(x)-1)) .
.
Dans le cas présent=\tan(\dfrac{3x}{2})) et
et =\tan(3x)) .
.
(f(x)-1)=\tan(3x)(\tan(\dfrac{3x}{2})-1) =\dfrac{\tan(\dfrac{3x}{2})-1}{\dfrac{1}{tan(3x)}) .
.
La limite de la dernière expression quand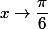 est de la forme
est de la forme  . La régle de l'Hôpital donne:
. La régle de l'Hôpital donne:
(f(x)-1)=\lim_{x \to \frac{\pi}{6}}\text{ }\dfrac{\frac{3}{2}[\tan^2(\dfrac{3x}{2})+1]}{(-3)\dfrac{1+tan^2(3x)}{tan^2(3x)}=......)
@Sheeppowa
Termines les calcules et conclus
Je vous propose de calculer
On a donc
On essaie de calculer
Comme
on peut alors écrire
Dans le cas présent
La limite de la dernière expression quand
@Sheeppowa
Termines les calcules et conclus
Et bein, ca s'est rapide, je vous remercie pour cette méthode plutôt efficace, et effectivement on retrouve la limite recherché qui est 1/e.
Mais j'aimerais pouvoir réussir cette exercice en utilisant les développements limités,car oui c est bien de savoir d'autres méthodes avec d'autres règles ( je ne connaissais pas la règle de l'hopital ) mais encore faut t-il que j'arrive à maitriser correctement les outils que je connais.
Je vous explique: je suis bloqué avec les développements limités, en effet, j'ai un terme qui s'écrit 1/tan(3h) et je ne suis pas en mesure de le calculer, je ne peut pas utiliser la formule 1/(1-g) car g doit avoir un terme constant nul et ce n'est pas le cas si on l'applique en faisant 1/[1-(1-tan(3h))].
Mais j'aimerais pouvoir réussir cette exercice en utilisant les développements limités,car oui c est bien de savoir d'autres méthodes avec d'autres règles ( je ne connaissais pas la règle de l'hopital ) mais encore faut t-il que j'arrive à maitriser correctement les outils que je connais.
Je vous explique: je suis bloqué avec les développements limités, en effet, j'ai un terme qui s'écrit 1/tan(3h) et je ne suis pas en mesure de le calculer, je ne peut pas utiliser la formule 1/(1-g) car g doit avoir un terme constant nul et ce n'est pas le cas si on l'applique en faisant 1/[1-(1-tan(3h))].
ln(f(x)) = tan(3x) * ln(tan(3x/2))
lim(x--> Pi/6) [tan(3x) * ln(tan(3x/2))] = lim(x--> Pi/6) [ln(tan(3x/2))/cotan(3x)] qui est de la forme 0/0 ---> application de la règle de Lhospital
= lim(x--> Pi/6) [(3/(2.cos²(3x/2).tan(3x/2)))/-(3/sin²(3x))] = lim(x--> Pi/6) [-sin²(3x)/sin(3x)] = lim(x--> Pi/6) [-sin(3x)] = -1
Et donc lim(x--> Pi/6) [ln(f(x)] = -1
---> lim(x--> Pi/6) f(x) = e^-1 = 1/e
Vive le Marquis de Lhospital ... même si on néglige d'enseigner sa méthode (va savoir pourquoi ?)
:zen:
lim(x--> Pi/6) [tan(3x) * ln(tan(3x/2))] = lim(x--> Pi/6) [ln(tan(3x/2))/cotan(3x)] qui est de la forme 0/0 ---> application de la règle de Lhospital
= lim(x--> Pi/6) [(3/(2.cos²(3x/2).tan(3x/2)))/-(3/sin²(3x))] = lim(x--> Pi/6) [-sin²(3x)/sin(3x)] = lim(x--> Pi/6) [-sin(3x)] = -1
Et donc lim(x--> Pi/6) [ln(f(x)] = -1
---> lim(x--> Pi/6) f(x) = e^-1 = 1/e
Vive le Marquis de Lhospital ... même si on néglige d'enseigner sa méthode (va savoir pourquoi ?)
:zen:
Archytas a écrit:D'ailleurs elle dit quoi sa règle ? Que lim f/g = lim f'/g' non ?
Oui, enfin à condition de ne pas oublier de vérifier si les conditions pour pouvoir appliquer cette règle sont bien réunies.
Mais si on prend (et c'est indispensable) le peine de vérifier si la règle est applicable ... et que c'est le cas, elle permet souvent d'arriver au but de manière rapide.
:zen:
 Re: calcul de limite
Re: calcul de limite
Ericovitchi a écrit:Oui il faut effectivement poser x=pi/6+h et puis après il faut faire des développements limités des fonctions (tan puis ln puis e^...) au voisinage de 0 (en commençant par écrire a^b=e^(blna)
C'est un peu long c'est sûr, on trouve f(h)=1/e+3h²/(2e)+o(h^4) qui montre que ça tend bien vers 1/e
desolé mais j'ai pas compris exactement ,tout ce que j'obtiens apres calcul du tg3h *ln(tg3h/2) c'est ln3h/2[3h+9h^3/3]+27h^3/4. l'exponentielle ne fonctionne pas dans ce cas . c'est la ou je bloque .
Si vous pouviez m'aider pour avoir le 1/e s'il vous plait
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
