Calcul intégral
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 18:13
par mehdi-128 » 28 Déc 2007, 18:13
Calcul intégral par la méthode des résidus
Rebonjour,je rebloque sur une autre intégrale ,ca serait sympa de me reaider: :stupid_in
sin(x)}{x(x^2+a)}dx)
Voila je vois pas comment partir ....
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 19:13
par trust » 28 Déc 2007, 19:13
essaie avec ça
e^{iz}dz}{z(z^2+a)}}) = \frac 12 Im( 2i\pi (res(\frac {(z^2-a)e^{iz}}{z(z^2+a)},0)+res(\frac {(z^2-a)e^{iz}}{z(z^2+a)},ia))))
si
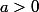
sinon
e^{iz}dz}{z(z^2+a)}}) = \frac 12 Im( 2i\pi (res(\frac {(z^2-a)e^{iz}}{z(z^2+a)},0)+res(\frac {(z^2-a)e^{iz}}{z(z^2+a)},-ia))))
si
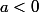
je te laisse pour le cas
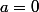
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 19:34
par mehdi-128 » 28 Déc 2007, 19:34
trust a écrit:essaie avec ça
e^{iz}dz}{z(z^2+a)}}) = \frac 12 Im( 2i\pi (res(\frac {(z^2-a)e^{iz}}{z(z^2+a)},0)+res(\frac {(z^2-a)e^{iz}}{z(z^2+a)},ia))))
si
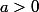
sinon
e^{iz}dz}{z(z^2+a)}}) = \frac 12 Im( 2i\pi (res(\frac {(z^2-a)e^{iz}}{z(z^2+a)},0)+res(\frac {(z^2-a)e^{iz}}{z(z^2+a)},-ia))))
si
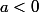
je te laisse pour le cas
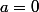
Merci,mais il y a un truc que j'ai pas compris:
Quel est le chemin selon lequel on intègre ?
Et on ne connait pas l'indice de 0, ia et -ia ...
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 19:41
par trust » 28 Déc 2007, 19:41
mehdi-128 a écrit:Merci,mais il y a un truc que j'ai pas compris:
z^2+a=0 z= ia ou z=-ia
et ca ne dépend pas du signe de a ?!
oui, le théorème des résidus dit qu'il ne faut prendre que les nombres à parties imaginaires positives
Et on ne connait pas l'indice de 0, ia et -ia
On n'en a pas trop besoin je crois ici...
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 19:44
par trust » 28 Déc 2007, 19:44
mehdi-128 a écrit:Quel est le chemin selon lequel on intègre ?
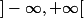
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 19:44
par mehdi-128 » 28 Déc 2007, 19:44
trust a écrit:oui, le théorème des résidus dit qu'il ne faut prendre que les nombres à parties imaginaires positives
On n'en a pas trop besoin je crois ici...
Euh j'ai pas capté la :le théorème des résidus dit que :
I=2iPi.Somme des résidus aux poles .Somme des Indices aux poles
donc comment faire sans connaitre les indices ,et comment connaitre les indices sans connaitre le chemin ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 19:55
par mehdi-128 » 28 Déc 2007, 19:55
Merci mais j'ai toujours un peu de mal c'est quand qu'on ne met pas les indices dans le théorème des résidus ?
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 19:59
par trust » 28 Déc 2007, 19:59
retourne le livre que jt'ai passé, p. 88 - 89
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 20:01
par mehdi-128 » 28 Déc 2007, 20:01
trust a écrit:retourne le livre que jt'ai passé, p. 88 - 89
Ah j'ai enfin trouvé ,merci beaucoup ....
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 20:06
par mehdi-128 » 28 Déc 2007, 20:06
Je trouve :
}{3a-1})
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 20:11
par trust » 28 Déc 2007, 20:11
dans quel cas?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 20:23
par mehdi-128 » 28 Déc 2007, 20:23
trust a écrit:dans quel cas?
pour a > 0 j'ai trouvé ce résultat ....
Une petite question en passant:dans le théorème on dit que Im(pole)>0 mais la partie imaginaire de 0=0 n'est pas strictement sup a 0?!
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 28 Déc 2007, 20:25
par trust » 28 Déc 2007, 20:25
cool :zen: oui c'est ça normalement...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 20:25
par mehdi-128 » 28 Déc 2007, 20:25
trust a écrit:cool :zen: oui c'est ça normalement...
Une petite question en passant:dans le théorème on dit que Im(pole)>0 mais la partie imaginaire de 0=0 n'est pas strictement sup a 0?!
-
petitrenard
- Messages: 1
- Enregistré le: 28 Déc 2007, 20:23
-
 par petitrenard » 28 Déc 2007, 20:46
par petitrenard » 28 Déc 2007, 20:46
trust a écrit:cool :zen: oui c'est ça normalement...
vrai pour a>0 :marteau:
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2007, 20:49
par mehdi-128 » 28 Déc 2007, 20:49
petitrenard a écrit:vrai pour a>0 :marteau:
Oui mais y a un truc qui me tracasse:le théorème utilisé stipule que :
im(pole)>0 or 0 est pole donc n'y at-il pas un pb ?
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 29 Déc 2007, 05:55
par trust » 29 Déc 2007, 05:55
c'est
 \geq 0)
.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 29 Déc 2007, 11:14
par mehdi-128 » 29 Déc 2007, 11:14
trust a écrit:c'est
 \geq 0)
.
Ah ouf merci j'ai eu peur ...
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 29 Déc 2007, 14:38
par Pythales » 29 Déc 2007, 14:38
Moi je touuve
)
ce qui n'est pas idiot a priori, car si

ou si

on retrouve la valeur de

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités