Bonjour, je rencontre des difficulté à comprendre cette exercice..
On note X une variable aléatoire à valeurs entières positives ou nulles dont la loi est décrite par le diagramme en bâtons ci-dessous :
Le tableau décrit les premiers coefficients de la loi X.
k 0 1 2 3 4
P(X=k) 0.0369 0.1217 0.2008 0.2209 0.1823
Quelle est la probabilité que X prenne une valeur strictement supérieure à 4 ?
0.2374. Bonne réponse.
X suit une loi de Poisson. Déduire des valeurs du tableau la valeur du paramètre de la loi de Poisson :
X suit la loi de Poisson de paramètre :
je ne sais pas comment déterminer le paramètre de la loi poisson..
Calcul avec une loi de Poisson
7 messages
- Page 1 sur 1
Re: Calcul avec une loi de Poisson
Bonjour,
Puisqu'on te dit que suit une loi de Poisson, tu sais ce que vaut
suit une loi de Poisson, tu sais ce que vaut 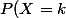) , en fonction de
, en fonction de  et du paramètre
et du paramètre  . Puisque tu connais
. Puisque tu connais 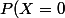, \ldots, P(X=4)) , tu peux identifier
, tu peux identifier  .
.
Puisqu'on te dit que
Re: Calcul avec une loi de Poisson
Bonjour,
 = P(X=k) = \frac{\lambda^k}{k!}.e^{-\lambda})
Avec k = 0, on a donc
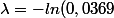 = 3,29954)
On peut vérifier si cela colle pour les autres valeurs de k.
k = 1 --> = P(X=1) = \frac{3,29954^1}{1!}.e^{-3,29954} = 0,12175...)
k = 2 --> = P(X=2) = \frac{3,29954^2}{2!}.e^{-3,29954} = 0,20086...)
k = 3 --> = P(X=3) = \frac{3,29954^3}{3!}.e^{-3,29954} = 0,22092...)
k = 4 --> = P(X=4) = \frac{3,29954^4}{4!}.e^{-3,29954} = 0,18223...)
C'est bon.

Avec k = 0, on a donc
On peut vérifier si cela colle pour les autres valeurs de k.
k = 1 -->
k = 2 -->
k = 3 -->
k = 4 -->
C'est bon.
Re: Calcul avec une loi de Poisson
Une nouvelle fois, Black Jack fait l'exercice à la place du questionneur, sans lui donner le temps de réfléchir aux indications que j'ai données.
Re: Calcul avec une loi de Poisson
Là c'est ben vrai ; c'est pas seulement une queue de poisson , c'est le poisson tout entier !
Re: Calcul avec une loi de Poisson
J'ai compris la méthode mais je comprends pas comment vous avez fait pour trouver la réponse final.
la valeur du plus grand que 4.
la valeur du plus grand que 4.
Black Jack a écrit:Bonjour,
Avec k = 0, on a donc
On peut vérifier si cela colle pour les autres valeurs de k.
k = 1 -->
k = 2 -->
k = 3 -->
k = 4 -->
C'est bon.
Re: Calcul avec une loi de Poisson
desicook a écrit:J'ai compris la méthode mais je comprends pas comment vous avez fait pour trouver la réponse final.
la valeur du plus grand que 4.Black Jack a écrit:Bonjour,
Avec k = 0, on a donc
On peut vérifier si cela colle pour les autres valeurs de k.
k = 1 -->
k = 2 -->
k = 3 -->
k = 4 -->
C'est bon.
Bonjour,
Ce n'est pas la valeur finale ... on peut la trouver directement.
P(X>4) = 1 - P(X=0) - P(X=1) - P(X=2) - P(X=3) - P(X=4)
P(X>4) = 1 - 0,0369 - 0,1217 - 0,2008 - 0,2209 - 0,1823 = 0,2374
Ce n'est vrai que parce que (précisé dans l'énoncé) : On note X une variable aléatoire à valeurs entières positives ou nulles.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
