Asymptote oblique

[zygomatique]

alors là pour une fois je me permets de ne pas être totalement d'accord ....

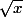
mais il est vrai qu'il faut jouer d'astuce et savoir bien calculer lorsqu'un ln(x) ou un se glisse au milieu ...

:lol3:

[laetidom]

Bonsoir,

division euclidienne de 2x²-5x+5 par x-1 donne 2x-3 avec un reste de 2

donc = 2x-3 +

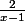
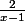
et comme ---> 0 quand x ---> +inf alors y = 2x-3 est asymptote oblique à Cf =====> voir graphe : http://www.cjoint.com/c/EKbt2u7Qy0f

[laetidom]

DEF asymptote oblique :

Si f(x) = ax + b + g(x), avec = 0

alors la droite d'équation y=ax+b est asymptote oblique de la courbe représentative de f en

[Dorian_pey]

Cela n'a absolument rien à voir mais pour étudier la derivabilite de (racine carré de x) * e^1-x ; sur l'intervalle ]0;+inf [ je tombe avec la formule f (x) - f (a) / x - a sur ( (racine de x) - (racine de a)/ x-a comment conclure alors svp ?

[Robot]

alors là pour une fois je me permets de ne pas être totalement d'accord ....

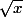
mais il est vrai qu'il faut jouer d'astuce et savoir bien calculer lorsqu'un ln(x) ou un se glisse au milieu ...

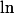
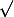
Faire une division euclidienne avec des et des demande sûrement beaucoup d'astuce ! :ptdr:

[zygomatique]

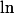
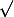
Faire une division euclidienne avec des et des demande sûrement beaucoup d'astuce ! :ptdr:

je mets trompé !!!! confondu avec une "décomposition en éléments simples" :lol3:

j'y ai pensé après avoir éteint l'ordi .... que j'avais dit une grosse con.... :mur: