Asymptote oblique

[Dorian_pey]

Bonsoir,
Je n'arrive pas à prouver que ma courbe Cf admet une asymptote oblique et je n'arrive pas à trouver son équation.. a l'aide !
Voici ma fonction f(x) =( 2x^2 -5x + 5)/(x-1) ; au cours de l'exercice j'ai déterminé le tableau de variation voilà
Merci d'avance

[Robot]

La recette : donne la pente de la direction asymptotique pour .
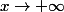
Si cette pente est , alors permet d'écrire l'équation de l'asymptote (si elle existe).

Je suis sûr que tout ça est dans ton cours.

[Dorian_pey]

Merci ! De mon cours je cite que : si f (x) - (ax+b) --> 0 en + ou - infini alors f admet une asymptote oblique d'équation y = ax+b ;
Mais n'ayant pas encore pratiqué cela en exercice je ne connais pas la méthode..

[Robot]

Merci ! De mon cours je cite que : si f (x) - (ax+b) --> 0 en + ou - infini alors f admet une asymptote oblique d'équation y = ax+b ;
Mais n'ayant pas encore pratiqué cela en exercice je ne connais pas la méthode..

Ca c'est la définition d'asymptote oblique. Tu es sûr qu'il n'y a aucun exemple dans ton cours, ni aucune indication sur le moyen de trouver a et b ?

[Dorian_pey]

Malheureusement non sinon j'aurais cherché ; bien que j'ai eu mon bac s je ne me souviens même pas avoir abordé les asymptotes obliques ou même en avoir rencontrées dans les annales

[Robot]

Bon ben je t'ai donné la recette dans mon premier message, tu peux y aller !

[Dorian_pey]

Ça marche j'arrive donc à Lim f (x) / x quand x --> +inf =0 ?

[Robot]

Non, non et non.

[Dorian_pey]

Soit je suis bidon ; je vais essayer de comprendre ou je fais faux ; quand je fais la limite de la fonction f (x) / x je tombe bien sûr une forme indéterminé du type inf / inf je mets alors en facteur x^2/x

[Dorian_pey]

Avant tout j'arrive avec (2x^2 -5x +5)/(x-1)x ? Ensuite je mets en facteur non ?

[Robot]

Que mets-tu en facteur ???

[Dorian_pey]

Le terme avec le plus gros exposant

[Dorian_pey]

Lim f (x)/x en + inf = 2

[Robot]

et alors ? c'est quoi le plus gros exposant au dénominateur de f(x)/x ?

Ah, tout de même !

[Dorian_pey]

J'ai oublié de simplifier ;)! Erreur toute bête.. ; ensuite j'ai donc mon ax ici 2x et pour trouver b je fais Lim f(x) - ax en + infi ?

[Dorian_pey]

A la fin j'arrive avec mon asymptote oblique y = 2x-7

[Robot]

Tu as dû faire une ou deux erreurs de signe dans ton dernier calcul.

[zygomatique]

salut

une autre recette assez classique : effectuer la division euclidienne du numérateur par le dénominateur ...

[Dorian_pey]

C'était bien 2x+5 alors ? J'ai modifié mon post 2 fois car je pensais m'être tromper ! Je ne sais pas si je connais encore ça mais je m'informer ais si jamais c'est plus rapide ! En tout cas merci

[Robot]

Recette qui ne s'applique qu'aux fractions rationnelles.