Approximation polynomiale de Arctan

[meloman0]

quelqu'un peut il m'aider ou me donner une methode pour l'approximation polynomiale de la fonction Arctan :hum:

merci

[Nightmare]

Salut,

au voisinage de 0, Arctan étant de classe Coo,

Il ne te reste qu'à calculer les dérivées successives de Arctan en 0. Tu remarqueras que la première dérivée est 1/(1+x²) et qu'on peut obtenir facilement un développement limité de celle-ci.

[meloman0]

je ne peux pas le faire car on a pas encore etudié le developpement limité mais j'ai trouvé dans un exercice qu'il faut commencer par simplifier :

n
sigma((-1)^k q^k)= 1-q+q^2-q^3+....+(-1)^n q^n
k=0

est ce que tu peux m'aider à le faire

[mathelot]

Bj,

développer comme somme d'une série géométrique
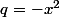
de raison puis intégrer

il appert que ce DSE ne fonctionne plus au dela de
et qu'ensuite on essaye avec arctan(1/x)