Application linéaire de R3

[Stevenson123]

Je tente quand même on sait jamais :









Donc on a ceci :



donc

[infernaleur]

Salut, oui ton raisonnement est juste.
Mais il y a une méthode beaucoup plus rapide une fois que tu as calculé et.

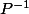
Tu a du voir normalement la formule de changement de base :
Soit B et C deux bases (de même dimension) d'un espace vectoriel E de dimension finie,
Soit f un endomorphisme sur E, on a :

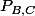
où désigne la matrice de passage de la base B vers la base C et désigne la matrice de l'endomorphisme f dans la base B

Donc dans ton exo toi en fait si on pose B la base canonique (e1,e2,e3) et C la base (v1,v2,v3)

Tu as :
Et donc comme tu cherche la matrice de f dans la base C tu as donc :



Il te reste plus qu'à faire un petit calcul matriciel et tu trouves la même chose normalement.

[Pseuda]

Bonsoir,

C'est ça, tu as compris. Tu verras (ou as vu) qu'on peut le faire aussi avec une formule de changement de base :

Si on a :
= matrice de l'application linéaire dans la base
= matrice de l'application linéaire dans la base
= matrice de passage de à

alors :

On fait les opérations de droite à gauche :
transforme les nouvelles composantes ( dans ) d'un vecteur en les anciennes ( dans ) :
calcule (avec les anciennes composantes des vecteurs dans , et on obtient avec ses anciennes composantes dans ) :
transforme les anciennes composantes obtenues (dans ) du vecteur en les nouvelles ( dans ) : .

Pas vu le message d'@infernaleur. Je laisse.

[Stevenson123]

Donc si je devais répondre de façon correct au niveau de la notation des matrices ça donnerait cela :

[Pseuda]

C'est ça. Mais il n'existe pas qu'une seule notation des matrices (ou même de quoi que ce soit en mathématiques). La matrice de passage de à se note aussi : . Si on gagne en précision, on perd en légèreté, et inversement.

[Stevenson123]

D'accord je note pour la notation .

Les exercices étant réussi pour ma part et fini je remercie tout le monde encore une fois pour votre aide. Sujet résolu donc