Application linéaire

[dragao93]

Bonsoir,

J'ai un peu de mal à comprendre comment montrer qu'une application est linéaire.
J'ai bien compris les conditions à vérifier :
1) f(x+y) = f(x) + f(y)
2) f(;)*x) = ;)*f(x)

J'aimerais avoir un exemple concret s'ils vous plais.

Soit F1 R^3>R^3 , (x,y,z) > (y+x , x+1)

Je calcule ;)F(u) = (;)y+;)x , ;)x+;))
Comment calculer maintenant F(;)u) ?

Je sais que la réponse est que F1 n'est pas une application linéaire.

Voici un autre exemple pour laquelle la réponse est que F2 en est une:

F2 R²>R² (x,y) > (y+x , x*y)

De même, je calcule ;)F(u) = (;)x+;)y , ;)xy)

Mais je ne sais toujours pas comment calculer F(;)u) ...


Pourriez-vous m'aider s'il vous le voulez bien ?

Je vous remercie par avance ;)

[Arnaud-29-31]

Bonsoir,

Attention, F2 n'est pas linéaire non plus.

En effet,



Si u = (x,y), alors



Alors que

Cela répond t-il à ta question ?

[dragao93]

Tout d'abord merci pour ta réponse rapide, c'est bien la réponse que j'attendais :)

Par contre il y a une étape que je ne comprends pas, je sais que ça doit être simple mais j'ai vraiment de grosses lacunes en maths.
Est-ce que tu pourrais me détailler le passage de F2(;)x,;)y) = (;)x+;)y , ;)x*;)y)

Est ce qu'il suffit de remplacer dans (x+y , x*y) en sachant que x=;)x et y=;)y?

Ca donne la même chose que toi donc je pense que c'est ça ..

Sinon, pour la 1ère, d'après ce que tu m'as expliqué , ça donnerait :

F1 : (x,y,z) --> (y+x , x+1)

1) ;)F(u) = (;)y+;)x , ;)x + ;))=(;)(x+y) , ;)(x+1))

2) F(;)u) = (;)y+;)x+;)x+;) , ;)y+;)x+1)=(;)(y+2x+1) , ;)(x+y+1)

>> pas une application linéaire.

Est-ce que c'est correct ?

Merci à toi ! :)

[Arnaud-29-31]

C'est comme en seconde quand on te donnait une fonction f := x -> x² + 1 par exemple.
On a f(x) = x² + 1 donc f(u) = u² + 1 ou encore ...


Pour ton première exemple, on a donc
On a bien comme tu l'as écris,
Par contre, ... Je ne vois pas où tu vas pécher les termes que tu as mis en trop ...

[Nightmare]

Salut,

pour ne pas trop se fatiguer à faire des calculs, on vérifie aisément dans les deux cas - celui de l'exercice et celui proposé par Arnaud - que l'application n'envoie pas 0 sur 0 ce qui est nécessaire pour une application linéaire.

[Arnaud-29-31]

Oui effectivement, pour montrer qu'une application n'est pas linéaire tu peux juste montrer qu'il y'a un truc qui cloche comme ce que propose Nightmare. Ca marche pour 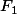mais pas pour 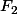: en effet 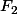envoie 0 sur 0 mais n'est pas linéaire (condition nécessaire mais pas suffisante)

Par contre pour montrer qu'une application est linéaire on montrera les deux conditions que tu cites.
A noter que pour gagner du temps on regroupera les deux en une et on montrera que

Après avec un peu d'habitude, on repère facilement les applications qui ne sont pas linéaire. Du genre s'il y a un carré qui traine, ou une multiplication entre deux variables ou un réel seul additionné ...

[dragao93]

ah ok je comprends mieux :)
J'ai saisi le truc.
Je vais essayer d'en faire d'autres en utilisant les 2 méthodes.
Merci à vous 2 ! :++: