Bonjour à tous,
Je ne comprends pas ce que signifie l'espace L1 et L2.
De plus, comment peut-on définir si une fonction ou une suite de fonction fait partie de cet ensemble? Existe t'il un lien entre l'appartenance de la fonction à l'ensemble (L1 ou L2) ainsi que la fonction en elle-même?
J'espère avoir été claire et vous remercie
Apartenance à l'ensemble L1 et L2
10 messages
- Page 1 sur 1
Re: Apartenance à l'ensemble L1 et L2
Bonjour,
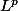 n'est pas exactement un ensemble de fonction, mais l'ensemble des fonctions mesurables, avec le module de la puissance piem qui posséde une intégrale finie, quotienter par la relation :
n'est pas exactement un ensemble de fonction, mais l'ensemble des fonctions mesurables, avec le module de la puissance piem qui posséde une intégrale finie, quotienter par la relation :

Ce qui fait que si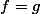 dans
dans 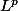 alors
alors  et non pas surment.
et non pas surment.
Voilà, voilà.
Ce qui fait que si
Voilà, voilà.
Re: Apartenance à l'ensemble L1 et L2
Merci de votre réponse. Cependant je dois avouer que ça reste encore flou à mes yeux.
Ce que je souhaite savoir c'est : pour une fonction donnée, par exemple : f(t) =x² . Cette fonction fait-elle partit de L1? Fait elle partit de L2? Et surtout, pourquoi oui ou non?
Merci d'avance.
Ce que je souhaite savoir c'est : pour une fonction donnée, par exemple : f(t) =x² . Cette fonction fait-elle partit de L1? Fait elle partit de L2? Et surtout, pourquoi oui ou non?
Merci d'avance.
Re: Apartenance à l'ensemble L1 et L2
f(x)=x^2 pour la fonction carrée.
 \text{ ssi } \int_{E} |g|^p \text{d}x<\infty)
Ainsi\cap L^1([0,1])) l'intégrale du module de la fonction carrée est finie sur [0,1], ainsi que son carré :
l'intégrale du module de la fonction carrée est finie sur [0,1], ainsi que son carré : | \text{ d}x <\infty) et
et |^2\text{ d}x <\infty)
mais n'estpas dans
n'estpas dans  \cup L^1(\mathbb R)) , ce n'est pas le cas sur
, ce n'est pas le cas sur  tout entier :
tout entier :
| \text{ d}x =\infty) et
et |^2\text{ d}x =\infty)
Ainsi
mais
Re: Apartenance à l'ensemble L1 et L2
Merci ça semble plus claire.
Si j'ai bien compris :
On peut dire que f(x)=x² appartient à L1 entre [0;1] car : \int |x²| dx donne un nombre réel.
En revanche sur l'interval [-inifi;+inifi] ceci n'est pas défini, donc x² n'appartient pas à L1 dans le limite ou l’intervalle de l'intégration n'est pas définie. A contre exemple, une constante est défini dans L1 et L2 donc?
Excusez moi, j'ai pas un de mal avec l'éditeur d'équation, j'espère être compréhensible
Si j'ai bien compris :
On peut dire que f(x)=x² appartient à L1 entre [0;1] car : \int |x²| dx donne un nombre réel.
En revanche sur l'interval [-inifi;+inifi] ceci n'est pas défini, donc x² n'appartient pas à L1 dans le limite ou l’intervalle de l'intégration n'est pas définie. A contre exemple, une constante est défini dans L1 et L2 donc?
Excusez moi, j'ai pas un de mal avec l'éditeur d'équation, j'espère être compréhensible
Re: Apartenance à l'ensemble L1 et L2
Oui, les constantes sont dans ) , mais pas dans
, mais pas dans ) .
.
Autre exemple :
=\frac{1}{\sqrt x}) est dans
est dans ) mais pas dans
mais pas dans )
Autre exemple :
Re: Apartenance à l'ensemble L1 et L2
Au sujet de h(x) : j'ai compris pourquoi ça appartient à L1, mais pourquoi ça n'appartient pas à L2 ?
Merci d'avance.
Merci d'avance.
Re: Apartenance à l'ensemble L1 et L2
Pour voir si cela appartient à ) , ils nous faut calculer :
, ils nous faut calculer : 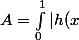|^2\text{ d}x)
or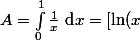]_0^1) qui n'est pas fini.
qui n'est pas fini.
or
Re: Apartenance à l'ensemble L1 et L2
D'accord, j'ai compris. 
Je vous remercie beaucoup pour vos explications, vous me sortez une épine du pied .
.
Bonne fin de journée
Je vous remercie beaucoup pour vos explications, vous me sortez une épine du pied
Bonne fin de journée
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
