Antisymétrie, juste ?

par **rifly01** » 06 Fév 2007, 23:20

Bonjour,

Je suis entrain de réviser les relations d'ordre ...
et je me bloque ici :

Soit

définie sur

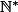
par :
[center]

[/center]
[/tex]

Montrer que

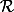
est relation antisymétrique.

==========

Ce que j'ai fait :

Soient

tels que

a-t-on x=y?

(je ne suis pas sûr

donc

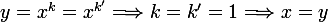
D'ou l'antisymétrie
C'est juste ?

Merci d'avance,

par **jose_latino** » 06 Fév 2007, 23:36

C'est incorrect,

rifly01 a écrit:
Merci d'avance,

C'est vraiment:

par **jose_latino** » 06 Fév 2007, 23:40

De même pour obtenir

rifly01 a écrit: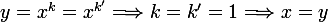

il faut faire attention au cas

ou

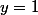
lequel, si bien c'est facile à vérifier, ce n'est pas possible utiliser le raisonement antérieur.

par **rifly01** » 07 Fév 2007, 00:28

Merci ,

Pour le cas y=1 => k=0, pareil pour x=1 => k'=0 donc R est une relation d'antisymétrie (dans ce cas)

Mais je ne vois pas dans les autres cas (x=/=1 v y=/=1) ...

par **rene38** » 07 Fév 2007, 00:36

Salut

rifly01 a écrit:Pour le cas y=1 => k=0, pareil pour x=1 => k'=0

ne serait pas un peu contradictoire avec

?

par **rifly01** » 07 Fév 2007, 00:37

Je refais ...

Si

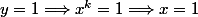
(ou k=0 mais on est dans N* donc exclu)

Si

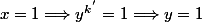
(ou k'=0 mais on est dans N* donc exclu)

Lorsque x=1 ou y=1 l'antisymétrie est vérifiée ...
C'est bon ?

Pour les autres cas je ne vois pas

Si

je ne vois pas la suite.

Je sais qu'on doit avoir kk'=1 mais je ne vois pas comment y parvenir

par **rene38** » 07 Fév 2007, 01:01

Je tente :

: 2 possibilités

et le problème est réglé.

donc

par **rifly01** » 07 Fév 2007, 02:00

Waw,

Merci bien rené38

Antisymétrie, juste ?

antisymétrie, juste ?

Qui est en ligne