Bonjour !
J'ai a peu près réussit la première questions, mais après...
Voici mon exo :
Soit (A,+,.) un anneau (avec unité).
Soit aA (fixé)
1)Montrer que l'application fa : x |----> a.x de (A,+) dans (A,+) est un endomorphisme de groupes.
2)On note (End(A),+,°) l'anneau des endomorphismes de (A,+) muni de l'opération de composition ° (rho).
Montrer que l'application # : a |----> fa de (A,+,°) dans (A,+,.) est un homomorphisme d'anneaux qui est injectif.
3)Supposons A=Z (Z l'ensemble des entiers relatifs)
Montrer que # est un isomorphisme d'anneaux et déterminer le groupe des éléments inversibles de (End(Z),+,°).
Voila !!!!
Si un illustre mathématicien passais par là, merci à lui !!!
Anneau, Endomorphisme, homomorphisme, je m'en sors plus !
7 messages
- Page 1 sur 1
Effectivement, voici l'énoncé de 2 (corrigé!):
2)On note (End(A),+,°) l'anneau des endomorphismes de (A,+) muni de l'opération de composition °.
Montrer que l'application de (A,+,.) dans End(A,+,°) est un homomorphisme d'anneaux qui est injectif.
de (A,+,.) dans End(A,+,°) est un homomorphisme d'anneaux qui est injectif.
(Et en fait, je suis pas du tout sur de moi pour la 1ère question.... If you can help me..)
2)On note (End(A),+,°) l'anneau des endomorphismes de (A,+) muni de l'opération de composition °.
Montrer que l'application
(Et en fait, je suis pas du tout sur de moi pour la 1ère question.... If you can help me..)
Pour le 3°
D'après les résultats précédents, on a est un endomorphisme de Z vers nd(Z ).
est un endomorphisme de Z vers nd(Z ).
Il est injectif. Pour montrer qu'il est isomorphisme d'anneaux, il faut considérer un endomorphisme de Z et prouver qu'il est de la forme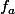 pour un certain entier
pour un certain entier  .
.
Soit donc un endomorphisme de Z , et posons
un endomorphisme de Z , et posons 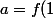) (c'est la seule possibilité logique, puisque on veut prouver que pour tout x,
(c'est la seule possibilité logique, puisque on veut prouver que pour tout x, =ax) ).
).
Comme est un endomorphisme du groupe (Z ,+), je peux écrire que
est un endomorphisme du groupe (Z ,+), je peux écrire que =f(1+1)=f(1)+f(1)=a+a=2a) et continuer par récurrence
et continuer par récurrence
De même pour=-f(1)=-a = -1\times a) et pour les entiers négatifs.
et pour les entiers négatifs.
J'ai bien prouvé que f était de la forme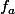
D'après les résultats précédents, on a
Il est injectif. Pour montrer qu'il est isomorphisme d'anneaux, il faut considérer un endomorphisme de Z et prouver qu'il est de la forme
Soit donc
Comme
De même pour
J'ai bien prouvé que f était de la forme
Okay pour le 3 !! (Merci Galt).
Par contre, pour le 2, je crois que ce que tu as fait n'est pas juste (a cause de l'énoncé, initialement faux!).
Voici la version modifiée :
2)On note (End(A),+,°) l'anneau des endomorphismes de (A,+) muni de l'opération de composition °.
Montrer que l'application de (A,+,.) dans (End(A),+,°) est un homomorphisme d'anneaux qui est injectif.
de (A,+,.) dans (End(A),+,°) est un homomorphisme d'anneaux qui est injectif.
Voila, normalement, là, il est bien écrit... Si vous voyez....
Par contre, pour le 2, je crois que ce que tu as fait n'est pas juste (a cause de l'énoncé, initialement faux!).
Voici la version modifiée :
2)On note (End(A),+,°) l'anneau des endomorphismes de (A,+) muni de l'opération de composition °.
Montrer que l'application
Voila, normalement, là, il est bien écrit... Si vous voyez....
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
