Homomorphisme bijectif
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 05 Avr 2008, 13:41
par raito123 » 05 Avr 2008, 13:41
Salut ,
Je viens de commencer un nouveau chapitre ( les structures algébriques ) et là je bloque sur un exo !!
Je dois montrer qu'il n'y a pas d'homomorphisme bijectif de
)
vers
)
Merci de m'aider ^^
Les multiples ne doivent pas être utilisés sans nécessité
 par alavacommejetepousse » 05 Avr 2008, 13:44
par alavacommejetepousse » 05 Avr 2008, 13:44
bonjour
un tel morphisme est parfaitement déterminé par a = f(1)
f(r) = a^r

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 05 Avr 2008, 13:46
par raito123 » 05 Avr 2008, 13:46
Tu peux expliquer j'ai pas compris
Les multiples ne doivent pas être utilisés sans nécessité
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Avr 2008, 13:47
par ThSQ » 05 Avr 2008, 13:47
Sinon 2 = f(a) = f(a/2+a/2) = f(a/2)^2 pour un a et pb

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 05 Avr 2008, 13:49
par raito123 » 05 Avr 2008, 13:49
ThSQ a écrit:Sinon 2 = f(a) = f(a/2+a/2) = f(a/2)^2 pour un a et pb
Et cela veut dire quoi exactement !!??
PS: Je commence ce chapitre tout seul (je ne vois pas trop ce que tu veux me dire )
Les multiples ne doivent pas être utilisés sans nécessité
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Avr 2008, 13:52
par ThSQ » 05 Avr 2008, 13:52
Ben si f est un isom entre Q,+ et Q*,* il existe a dans Q tel que f(a) = 2
Alors :
f(a) = f(a/2 + a/2) (clair ;))
= f(a/2) * f(a/2) (bicose morphisme)
= f(a/2)^2
= 2
Et 2 admettrait un racine carrée dans Q.
 par alavacommejetepousse » 05 Avr 2008, 13:53
par alavacommejetepousse » 05 Avr 2008, 13:53
f(1) = a
p entier positif strict
f(p) = f(1+...+1) = a^p
q entier positif strict
f(1) = f(1/q +....1/q) = f(1/q)^q donc f(1/q) = a^(1/q) puis
f (r) = a^r avec r = p/q >0
et f(-r) = 1/f(r) = 1/a^r = a^(-r)
f(r) = a^r ne saurait être une bijection (regarder de façon précise)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 05 Avr 2008, 14:13
par raito123 » 05 Avr 2008, 14:13
Ok c'est donc comme une procédure par absurde ou on suppose que s'il existe un tel morphisme alors il y aurait une contradiction !!!
ThSQ merci j'ai bien compris ta méthode :++: !!
alavacommejetepousse a écrit:f (r) = a^r avec r = p/q >0
et f(-r) = 1/f(r) = 1/a^r = a^(-r)
f(r) = a^r ne saurait être une bijection (regarder de façon précise)
Je ne vois pas comment elle ne pourait être une bijection !!
Atta peut-être une disjonction de cas ( a > 1 et a < 1 ) ! c'est ça ??!!
Merci
Les multiples ne doivent pas être utilisés sans nécessité
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Avr 2008, 16:49
par ThSQ » 05 Avr 2008, 16:49
raito123 a écrit:ThSQ merci j'ai bien compris ta méthode :++: !!
Cool :zen:
J'en propose une autre à ta sagacité :
(Q*,*) possède en élément d'ordre 2 (à savoir -1) tandis que dans (Q,+) n'a aucun élément d'ordre fini (sauf 0 mais bon) : donc pas d'isomorphisme possible
Dans le même genre, un exo trouvé dans un rapport d'oraux ENS : (Z,+) et (Z²,+) sont-ils isomorphes ?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 05 Avr 2008, 20:06
par raito123 » 05 Avr 2008, 20:06
(Dsl j'avais un cours d'anglais)
J'avais pas compris ce que ça veut "l'ordre d'un élément" et "element d'ordre fini" et par une petite recherche rapide j'obtiens :
"On appelle ordre d'un élément d'un groupe fini l'ordre (G , * ) l'ordre du sous-groupe engendré dans G par cet élément. "
Tu peux stp m'expliquer !!??
Les multiples ne doivent pas être utilisés sans nécessité
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Avr 2008, 21:24
par ThSQ » 05 Avr 2008, 21:24
C'est aussi (de manière équivalente) le plus petit n > 0 tq x^n = e (si un tel n n'existe pas on parle d'ordre infini).
Si tu veux continuer va falloir investir dans un cours raito !
http://www.les-mathematiques.net/b/c/a/node1.php3

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 05 Avr 2008, 21:33
par raito123 » 05 Avr 2008, 21:33
Ok je vais lire le cours ThSQ :lol4:
ThSQ a écrit:Dans le même genre, un exo trouvé dans un rapport d'oraux ENS : (Z,+) et (Z²,+) sont-ils isomorphes
ça suffit de dire qu'il n'y a pas d'application bijective ni de

ni de

pour montrer qu'on a pas d'isomorphismes ?
Les multiples ne doivent pas être utilisés sans nécessité
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 05 Avr 2008, 21:38
par ffpower » 05 Avr 2008, 21:38
Ca suffirait mais c est faux..
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Avr 2008, 21:38
par ThSQ » 05 Avr 2008, 21:38
raito123 a écrit:ça suffit de dire qu'il n'y a pas d'application bijective ni de

ni de

pour montrer qu'on a pas d'isomorphismes ?
Ca suffirait mais c'est faux

Z² et Z
sont en bijection
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 05 Avr 2008, 21:39
par ffpower » 05 Avr 2008, 21:39
..............
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Avr 2008, 21:47
par ThSQ » 05 Avr 2008, 21:47
Les mêmes mots à la même seconde !
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 06 Avr 2008, 09:10
par aviateurpilot » 06 Avr 2008, 09:10
Z et Z² sont bien ont bijection.
en effet: on prend pour
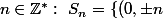,(\pm n,0),(a,b)\in Z^2:\ ab=n\})
et
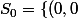\})
.
on peux ecrire (puisque

est fini)
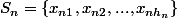
.
on prend
=i/2)
si

pair, et
=-\frac{i+1}{2})
si

impair.

est bijective
soit

tel que:
=(0,0))
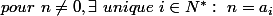
et dans ce cas
=f(a(i))=x_{n,c})
si et seulement si
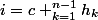
avec

.

est bien bijective.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 11 Avr 2008, 23:35
par raito123 » 11 Avr 2008, 23:35
Aziz j'ai compris la methode avec l'echequier mais là je ne comprend rien :briques: !!!
Quelqu'un connait une application de Z --> Z² ( juste pour info )
Les multiples ne doivent pas être utilisés sans nécessité
 par busard_des_roseaux » 12 Avr 2008, 07:15
par busard_des_roseaux » 12 Avr 2008, 07:15
[quote="raito123"]Aziz j'ai compris la methode
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités