Bonjour tout le monde .
Je suis étudiant en première année de physique , et nouveau sur le forum (alors que mes lacunes en maths datent ...)
Je ne comprends pas un point de mon cours d'analyse :
J(f) est la matrice jacobienne de f
f et g sont deux fonctions
Il est écrit J(fog)(x,y) = J(f) (g(x,y)) x J(f(x,y))
Mais je ne comprends pas exactement comment faire :
Je sais calculer J(f)(x,y) et J(g)(x,y) , mais comment fait on J(f) (g(x,y)
Aussi , y a t'il une différence entre J(f(x,y)) et J(f)(x,y) ? Les deux notations sont elles correctes ?
Faut il faire une dérivée de F par rapport à g(x,y) ? Auquel cas comment cela se fait il formellement ?
Merci d'éclairer ma lanterne
Analyse : Jacobienne de f o g
5 messages
- Page 1 sur 1
En effet ,
En effet, ma formule n'était pas correcte , merci à toi nyth .
Mais , vos réponses n'ont pas achevé de me faire comprendre. En effet , j'ai
J(FoG) = J(F)(g(x,y)) x J(G)(x,y) si j'ai bien saisi.
Mais comment appliquer J(F)(g(x,y)) , notation que je ne comprends pas
Dois je multiplier J(F)(x,y) par g(x,y) puis par J(G)(x,y)?
Mais , vos réponses n'ont pas achevé de me faire comprendre. En effet , j'ai
J(FoG) = J(F)(g(x,y)) x J(G)(x,y) si j'ai bien saisi.
Mais comment appliquer J(F)(g(x,y)) , notation que je ne comprends pas
Dois je multiplier J(F)(x,y) par g(x,y) puis par J(G)(x,y)?
bjr,
soit la fonction réelle toute simple

et la non moins simple fonction
)
La différentielle de f , notée df(x) est l'application linéaire:

La différentielle de g , notée dg(y) est l'application linéaire:
k)
gof est la fonction
)
Sa différentielle est
2xh = dg(y). df(x)(h))
elle s'écrit comme composée de deux applications linéaires
les coefficients étant calculé en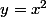 et en
et en  .
.
soit la fonction réelle toute simple
et la non moins simple fonction
La différentielle de f , notée df(x) est l'application linéaire:
La différentielle de g , notée dg(y) est l'application linéaire:
gof est la fonction
Sa différentielle est
elle s'écrit comme composée de deux applications linéaires
les coefficients étant calculé en
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
