Algèbre : preuve sur les cardinaux.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 05 Juin 2006, 08:53
par Zebulon » 05 Juin 2006, 08:53
Bonjour,
voici l'énoncé de ce qui me pose problème :
Soient H et K deux sous-groupes d'un groupe fini G, avec K inclus dans le normalisateur de H.
Montrer que
={card(H).card(K)\over{card({H\cap{K})}})
.
J'ai cherché à montrer que

définie comme suit est une bijection :

X(H\cap{K})\rightarrow{HXK}<br />\\(hk,x)\mapsto(hx,kx))
C'est clairement surjectif, mais pour l'injectivité je n'ai aucune idée...
Pourriez-vous m'aider s'il vous plaît?
Merci d'avance!
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 05 Juin 2006, 10:57
par alben » 05 Juin 2006, 10:57
Bonjour,
Es-tu sûr que ta fonction soit bien définie ?
Si z HK, il existe h,k tels que hk=z mais aussi h'k'. Il faudrait montrer que h'x=hx
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 05 Juin 2006, 11:02
par Zebulon » 05 Juin 2006, 11:02
J'avoue que je suis complètement perdue sur cet exercice. Je n'ai pas l'impression qu'introduire cette application soit une bonne idée.
Avez-vous d'autres idées?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Juin 2006, 11:21
par yos » 05 Juin 2006, 11:21
Je pense aussi que ta fonction est mal définie. car un élément de HK s'écrit de diverses façons sous la forme hk. C'est même le noeud du problème car si cette écriture était unique, on aurait HXK isomorphe à HK.
Je pense que l'inclusion de K dans
)
entraîne que HK est un sous groupe de G et on doit pouvoir l'exploiter.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 05 Juin 2006, 11:58
par Zebulon » 05 Juin 2006, 11:58
En effet, HK est stable par la loi :
si z et z' appartiennent à HK, alors il existe h, h' appartenant à H et k, k' appartenant à K tels que z=hk et z'=h'k' donc zz'=hkh'k'=hh''kk' car kH=Hk donc zz' appartient bien à HK.
Pour l'élément neutre, comme H et K sont des sous-groupes de G, e appartient à H et à K donc e=ee appartient à HK.
Pour l'inverse, soit z appartenant à HK, alors il existe h et k appartenant à H et K tels que z=hk et on sait qu'il existe
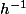
dans H et
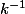
dans K et

et il existe un h' tel que

donc

appartient à HK.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Juin 2006, 12:42
par yos » 05 Juin 2006, 12:42
Tu dois pouvoir montrer

-
Amine.MASS
- Membre Naturel
- Messages: 65
- Enregistré le: 26 Avr 2006, 19:07
-
 par Amine.MASS » 05 Juin 2006, 19:48
par Amine.MASS » 05 Juin 2006, 19:48
bonsoir,
soit

X(K)\rightarrow{HK}<br />\\(h,k)\mapsto hk)
pour

,on montre que l'ensemble des antécédants de z par

est A={
 avec t \in H\cap K)
}
puis on utilise le principe des bergers pour conclure que
={card(H).card(K)\over{card({H\cap{K})}})
on pose B l'ensemble des antecédants de z,
*il est simple de vérifier que A est dans B
*soit (x,y)

B:
donc xy=hk d'ou
^{-1})
on pose

on a

et on a
=(ht,t^{-1}k))
donc
\in A)
dou...
allez bon courage :++:
Amine
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 06 Juin 2006, 08:30
par Zebulon » 06 Juin 2006, 08:30
Merci Amine, mais pouvez-vous m'énoncer le principe des bergers s'il vous plait? Je ne connais pas.
Merci d'avance.
-
Amine.MASS
- Membre Naturel
- Messages: 65
- Enregistré le: 26 Avr 2006, 19:07
-
 par Amine.MASS » 06 Juin 2006, 08:45
par Amine.MASS » 06 Juin 2006, 08:45
Zebulon a écrit:Merci Amine, mais pouvez-vous m'énoncer le principe des bergers s'il vous plait? Je ne connais pas.
Merci d'avance.
bonjour,
je croyais qu'on l'enseignait désolé:
soit f une application entre deux ensembles fini H et F,
si il existe

tq qlq soit
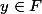
)=r)
,alors Card(H)=r.Card(F)
Cordialement,Amine
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
