Algèbre multilinéaire

par **minidiane** » 22 Fév 2009, 15:48

Bonjour,

je suis bloqué pour un exercice voici l'exercice:

Pour A,B appartenant à Mn(R) on définit
=Tr(tAB) (t=transposé)
1) Montrer que < , > est un produit scalaire sur Mn(R). Qu'elle est sa norme associée?

Je ne sais pas comment trouver sa norme.

2) Décrire l'orthogonale de la droite RIn où In est la matrice identité.

3) Montrer que les sous-espaces Sn(R) et An(R) (désignant les matrices symétriques et antisymétriques) sont orthogonaux. Calculer la projection orthogonale sur ces deux espaces.

Ces deux dernières questions je ne sais pas les faire.
Pourriez vous m'aider svp?
Merci

par **Joker62** » 22 Fév 2009, 16:08

Haileau ;)
On va faire dans l'ordre déjà :o

La norme associée à un produit scalaire ?
N(x) = Racine( )
Calcul < A ; A > c'est à dire Tr( tA . A )
Et là pas de secret : faut mettre les mains dans le camboui
Ecrit le terme de la ligne i;j de la matrice tA.A et fait la somme des éléments diagonaux.

par **minidiane** » 22 Fév 2009, 16:28

J'ai

Comme Tr(A)=Tr(tA)

j'obtiens:

enfin je pense

est-ce que cela est juste?

par **Joker62** » 22 Fév 2009, 16:38

Hum bé

Donc

Et ainsi les coeff diagonaux sont :

Reste plus qu'à sommer pour i allant de 1 à n et on doit retrouver ton bazarre en effet

par **minidiane** » 22 Fév 2009, 16:44

Donc la norme c'est la racine carré de cette somme?

par **leon1789** » 22 Fév 2009, 16:47

Joker62 a écrit:Hum bé

Donc
Et ainsi les coeff diagonaux sont :

Reste plus qu'à sommer pour i allant de 1 à n et..

et on retombe sur la somme des carrés des éléments de la matrice.

par **leon1789** » 22 Fév 2009, 16:48

minidiane a écrit:Donc la norme c'est la racine carré de cette somme?

oui, exactement comme

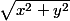
est une norme de (x,y)...

par **minidiane** » 22 Fév 2009, 16:51

D'accord merci, par contre on ne peut pas simplifier

par **leon1789** » 22 Fév 2009, 16:52

minidiane a écrit:D'accord merci, par contre on ne peut pas simplifier

tu penses à simplifier quoi ?

par **minidiane** » 22 Fév 2009, 16:54

ben je ne sais pas lol, en fait je pense que c'est bon comme ça

Pour la 2ème question as tu une suggestion pour décrire l'orthogonal?

par **Joker62** » 22 Fév 2009, 17:00

Non mais en fait y'a aucune simplification
Comme on te l'as fait remarqué c'est la somme des carrées des éléments de la matrice

En gros c'est la norme euclidienne quand on a identifier Mn(R) à R^(n^2)

Pour la deuxième question, il faut revenir à la définition de l'orthogonal
Soit V =
A appartient à l'orthogonale de V si et seulement si = 0 pour tout B dans V

par **minidiane** » 22 Fév 2009, 17:08

ok

Donc si

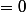
j'ai

d'où

Mais je ne vois pas ce que je peux conclure

par **leon1789** » 22 Fév 2009, 17:16

minidiane a écrit:ok

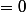
Donc si j'ai

d'où

Mais je ne vois pas ce que je peux conclure

N'oublies pas que tu cherches l'orthogonal de A = Id...

par **minidiane** » 22 Fév 2009, 17:23

je dois dire que là je suis un peu perdu, je ne vois as trop comment faire :hum:

par **Joker62** » 22 Fév 2009, 18:14

On cherche l'orthogonal de V = R. In
Soit B un élément de V c'est à dire il existe un a dans R tel que B ne comporte que des a sur la diagonale et des 0 ailleurs.

A est dans l'orthogonal si et seulement si = 0 <=> = 0
Continues sur cette voie

par **minidiane** » 22 Fév 2009, 18:28

Il faudrait que la matrice A soit nulle?
Vu que la matrice B est diagonale

par **Joker62** » 22 Fév 2009, 18:33

Euhhh
Vu que ???
Tu tires des conclusions hatives comme ça tout le temps ?

Fait le calcul moi j'ai pas de crayon et la mémoire vive de mon cerveau est en stand by :o

Ecris le produit scalaire proposé, et trouve une condition nécessaire sur A
Vérifie qu'elle est suffisante après

par **minidiane** » 22 Fév 2009, 18:43

:mur: Ben j'essaye de trouver mais je n'y arrive pas :mur:

comme le produit scalaire c'est la trace ici, si j'ai bien compris on multiplie a*x+a*y+...+a*z et cela doit faire 0. (où: x,y,...,z sont des nombre réel sur la diagonale de A)

il faut que les thermes qui sont sur la diagonale de A soit nul.

par **leon1789** » 22 Fév 2009, 18:49

minidiane a écrit::mur: Ben j'essaye de trouver mais je n'y arrive pas :mur:

comme le produit scalaire c'est la trace ici, si j'ai bien compris on multiplie a*x+a*y+...+a*z et cela doit faire 0. (où: x,y,...,z sont des nombre réel sur la diagonale de A)

il faut que les thermes qui sont sur la diagonale de A soit nul.

les thermes, c'est pour les curistes :id: ok, on considère les termes qui sont sur la diagonale.
D'abord Tu dis >, ok !
puis >
Quel est le lien logique entre les deux ?

par **Joker62** » 22 Fév 2009, 18:49

x,y,...,z sont pas forcément positifs

En fait il faut et il suffit juste que x+y+...+z = 0 c'est à dire la trace de la matrice soit nulle.

On le voyait comme ça :
Tr(tA.aIn) = aTr(tA.In) = aTr(tA) = aTr(A) qui s'annule si et seulement si Tr(A) vaut 0 (a non nul)

Edit : Sorry Léon

Algèbre multilinéaire

algèbre multilinéaire

Qui est en ligne