Salut,
Charlie a écrit:peut-on avoir une matrice A non diagonalisable de valeurs propres différentes de 0 tel que A^3 est diagonalisable ? (cela me paraîtrait bizarre au vu de la décomposition de Jordan)
Vu que tu parle de décomposition de Jordan, on peut éventuellement supposer que tu te place sur C, mais comme tu ne précise rien, je préfère donner la réponse générale : ça dépend du corps de base sur lequel on se situe.
- Sur un corps non algébriquement clos comme R c'est évidement possible : dans R^2 la matrice A d'une rotation vectorielle d'angle 2pi/n (
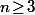
) est non diagonalisable car à valeur propres complexes et pourtant A^n=Id.
- Sur un corps de caractéristique finie

(même s'il est algébriquement clos) c'est aussi possible :

est non diagonalisable mais

- Par contre, sur un corps algébriquement clos
ET de caractéristique nulle, c'est impossible et c'est évident au vue de la décomposition de Jordan.
Charlie a écrit:Si une matrice est diagonalisable, peut-on trouver une base telle que dans cette base la matrice soit triangulaire supérieure avec les termes au-dessus de la diagonale non tous nuls ?
Bien sûr que oui : si tu part dans l'autre sens d'une matrice triangulaire avec des termes sur la diagonale tous différents mais absolument n'importe quoi au dessus de la diagonale alors le polynôme caractéristique sera scindé et à racines simple donc la matrice sera diagonalisable.
Par contre, à l'opposé, si tout les termes de la diagonale sont égaux à un certain lambda, la réponse devient "bien sûr que non" vu que dans ce cas ta matrice possède une unique valeur propre lambda et donc, si elle était diagonalisable, elle serait égale à lambda.Id et donc elle serait diagonale dans absolument n'importe quelle base donc en particulier elle doit déjà l'être dans la base "de départ" où on nous a donné la matrice.
