13 résultats trouvés
Revenir à la recherche avancée
Merci ! J'ai bien compris comment tu t'y es pris. Construire un exemple d'espace de probabilité sur lequel il existe deux événements A et B tels que P(A \cap B) - P(A)P(B) = \frac {1}{4} Je trouve ceci : Je me dis que \frac {1}{2} - \frac {1}{4} = \frac {1}{4} Il faut que je ...
- 13 Mai 2013, 12:36
- Forum: ✯✎ Supérieur
- Sujet: Inégalité en probabilité
- Réponses: 3
- Vues: 612
Inégalité en probabilité
Hello, Il y a une égalité que je n'arrive pas à démontrer : |P(A \cap B) - P(A)P(B) | \le \frac {1}{4} A et B deux événements de (\Omega,P) et on suppose que P(B) \in ]0,1[ J'ai essayé la formule des probabilités totales mais je n'aboutis à rien. Merci
- 12 Mai 2013, 17:07
- Forum: ✯✎ Supérieur
- Sujet: Inégalité en probabilité
- Réponses: 3
- Vues: 612
J'ai réussi à transformer l'écriture : Quand k>0 P(XZ=k \cap Y=1 \cap Z=1) = P((X=k \cap Y=1) \cap Z=1) = P(X = k \cap Z=1) = P(X=k)P(Z=1) P(XZ=k \cap Y=0 \cap Z=1) = P((X=k \cap Y=0) \cap Z=1) =P(X=-k \cap Z=1) = P(...
- 11 Mai 2013, 14:04
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
J'arrive pas à calculer les intersections..
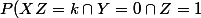=P(X=k \cap Y=0 \cap Z=1))
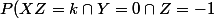)
et ainsi de suite.
J'ai essayé en conditionnant (X=k et Y=0) et ça mène à rien.
et ainsi de suite.
J'ai essayé en conditionnant (X=k et Y=0) et ça mène à rien.
- 10 Mai 2013, 17:29
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
Ok pour la loi XZ. Je n'ai vu que que les cas 1 et -1 car je pensais qu'on prenait que l'intersection des deux ensembles d'arrivés. P(XZ=k \cap Z=1) = P(X=k \cap Z=1)=P(X=k)(Z=1)=P(XZ=k)(Z=1) Même chose pour Z=-1. Les v.a sont indépendantes. Seulement,...
- 10 Mai 2013, 12:37
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
D'après la loi de XZ on peut dire :
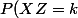=P(X=k) \forall k \in \{-1,1\})
X et Z sont indépendantes implique que XZ et Z sont indépendantes.
C'est ça ?
X et Z sont indépendantes implique que XZ et Z sont indépendantes.
C'est ça ?
- 10 Mai 2013, 10:11
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
Concernant la probabilité uniforme, je pensais qu'il s'agissait de la variable Y. Pour la loi de XZ je trouve : (XZ=1) = (X=1 \cap Z=1) \cup (X=-1 \cap Z=-1) Les événements sont disjoints et étant donné que X et Z sont indépendantes on a : P(XZ=1) = P(X=1 \cap Z=1...
- 09 Mai 2013, 19:20
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
Merci j'ai bien saisi cette question 2. Finalement c'était bien P(Y=1)=P(Y=0)=1/2.. Mais la manière dont je voyais les choses était correct à ce propos non ? Probabilité uniforme P(Y=1)= \frac {Card(X>0)}{Card(|X|(\Omega))} = \frac {9}{18} = \frac {1}{2} avec X > 0 = ...
- 09 Mai 2013, 16:09
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
Merci pour tes réponses ! Pour le (1) je viens de m'apercevoir que je n'ai pas répondu à la question : j'ai donné la loi de X, qui est par ailleurs, gentiment donné dans l'exercice pour justement trouver la loi de |X|.. Donc le (1), c'est bon c'est bien compris. P(|X|=k) = P(X=k U X=-k). Maintenant ...
- 09 Mai 2013, 15:25
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
Une chose : ce n'est pas plutôt \mathrm P(|X|=k \cap Y=1) = P(|X|=k) = \frac {P(X=k)}{2} ? Car l'image de |X| à 9 éléments et l'image de X en possède 18. D'où la division par 2. J'espère que je ne dis pas n'importe quoi.. Je trouve ceci : \mathrm P(|X|=k \cap Y=1) = \...
- 08 Mai 2013, 20:18
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
Merci pour la réponse. \mathrm P(|X| = k) = \begin{cases} \mathrm P(X=k \cup X=-k) \text si k \in X(\Omega) \\ 0 \end{cases} Ca j'ai bien compris, si k <0, c'est l'évènement impossible et ça vaut 0. Mais pourquoi : \mathrm P(|X| = k \cap Y=1) = P(X = k) ? C'es...
- 08 Mai 2013, 16:11
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
Vaut mieux oublier Sarrus... Outre les erreurs de calcul, ça ne fonctionne que pour les déterminants des matrices carrées d'ordre 3. L'idée c'est d'utiliser les propriétés sur les lignes et les colonnes de sorte à simplifier le déterminant. Exemple avec ton cas : \begin{vmatrix} 5 - \lambda & 5 ...
- 08 Mai 2013, 14:42
- Forum: ✯✎ Supérieur
- Sujet: Matrice
- Réponses: 10
- Vues: 594
v.a indépendantes
Bonjour à tous, J'aurai besoin d'aide pour cet exercice car j'ai beaucoup de mal à appliquer les propriétés sur l'indépendance sur les v.a Soit X : ;) -> {-9,-8,..,-1};){1,...,9} telle que pour tout entier k satisfaisant |k| \le 9 on a : P(X=k) = \frac {|k|}{90} On pose Y = 1 {X>0} (je ne sa...
- 08 Mai 2013, 13:31
- Forum: ✯✎ Supérieur
- Sujet: v.a indépendantes
- Réponses: 18
- Vues: 953
- 13 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
