Inégalité en probabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nedsrark
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Mai 2013, 12:11
-
 par nedsrark » 12 Mai 2013, 17:07
par nedsrark » 12 Mai 2013, 17:07
Hello,
Il y a une égalité que je n'arrive pas à démontrer :
 - P(A)P(B) | \le \frac {1}{4})
A et B deux événements de
)
et on suppose que
 \in ]0,1[)
J'ai essayé la formule des probabilités totales mais je n'aboutis à rien.
Merci
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Mai 2013, 20:27
par girdav » 12 Mai 2013, 20:27
-
nedsrark
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Mai 2013, 12:11
-
 par nedsrark » 13 Mai 2013, 12:36
par nedsrark » 13 Mai 2013, 12:36
Merci ! J'ai bien compris comment tu t'y es pris.
Construire un exemple d'espace de probabilité sur lequel il existe deux événements A et B tels que
 - P(A)P(B) = \frac {1}{4})
Je trouve ceci :
Je me dis que
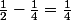
Il faut que je trouve
 = \frac {1}{2})
et
P(B) = \frac {1}{4})
En posant
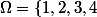
On détermine les évènements
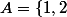
et
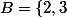
 = P(\{1,3}\) = \frac {1}{2})
 = P(\{1,2}\) = \frac {2}{4} = \frac {1}{2})
et
 = \frac {1}{2})
Ce qui nous fait bien
 - P(A)P(B) = \frac {1}{2} - \frac {1}{4} = \frac {1}{4})
J'ai une dernière question que je n'arrive pas à résoudre.
On a
 = \frac {2}{5} P(A|B) + \frac {3}{5} P(B|A^c))
avec
 < 1 \forall B \in \Omega)
J'ai démontré que Q est bien une loi de probabilité de

.
Mais on me demande à quelle condition sur
)
on a
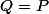
En fait je n'arrive pas à interpréter l'égalité.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 13 Mai 2013, 14:24
par Doraki » 13 Mai 2013, 14:24
si A = {1,2} et B = {2,3}, A inter B ça fait {2} et pas {1,3}.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités