8 résultats trouvés
Revenir à la recherche avancée
Je trouve bien comme module pour les 2 : 1/cos(\theta) De ce fait grâce a votre formule je trouve: cos(arg(z))= sin (\theta) Et sin(arg(z))= cos (\theta) Est ce possible ? Car je ne peux pas mettre sous la forme trigo ce genre d'arguments? Et ds la consigne il est écrit : 1 a...
- 12 Mar 2013, 11:48
- Forum: ✎✎ Lycée
- Sujet: probleme equation differentielle
- Réponses: 16
- Vues: 1249
j'ai essayé différentes méthodes pour faire disparaitre la racine, j'ai par exemple essayé de multiplier numérateur et dénominateur par : (tan^2(\theta) - 1^2) pour essayer de faire apparaitre une identité r. mais du coup je me retrouve avec le même pb au dénominateur.. J'ai égalemen...
- 06 Mar 2013, 18:53
- Forum: ✎✎ Lycée
- Sujet: probleme equation differentielle
- Réponses: 16
- Vues: 1249
- 06 Mar 2013, 12:49
- Forum: ✎✎ Lycée
- Sujet: probleme equation differentielle
- Réponses: 16
- Vues: 1249
/z_2/ = /z_1/ = V(tan^2(\theta) + 1^2) /z_2/ = /z_1/ = tan(\theta) + 1 LE problème est que normalement pour calculer les arguments, j'ai appris a faire cos(\theta)=PArtieReelle/module ET sin(\theta)=PArtieIm/module J'ai le droit de faire la même chose ici ? p...
- 06 Mar 2013, 11:53
- Forum: ✎✎ Lycée
- Sujet: probleme equation differentielle
- Réponses: 16
- Vues: 1249
Je me suis trompé dans mon a !!!
Donc enfaite mon premier calcul était le bon j'avais juste oublié le i dans la formule !
Merci, je re-recommence !
Donc enfaite mon premier calcul était le bon j'avais juste oublié le i dans la formule !
Merci, je re-recommence !
- 06 Mar 2013, 11:34
- Forum: ✎✎ Lycée
- Sujet: probleme equation differentielle
- Réponses: 16
- Vues: 1249
Autant pour moi j'ai fait n'importe quoi ! Cette fois je trouve pour les racines : Z1=[2sin(\theta*cos(\theta) +iV(4cos^4(\theta) ]/ (2cos(\theta) Z1=sin(\theta) + [i 2cos^2(\theta)] / (2cos(\theta)) Z1=sin(\theta) + icos...
- 06 Mar 2013, 11:22
- Forum: ✎✎ Lycée
- Sujet: probleme equation differentielle
- Réponses: 16
- Vues: 1249
Merci pour tout.
Du coup je trouve pour les racines:
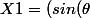/cos(\theta) ) - 1)
et donc pareil pour X2 mais avec un "+"
Cela vous semble t-il bon ? car je ne suis pas sûre de toutes mes simplifications..
Du coup je trouve pour les racines:
et donc pareil pour X2 mais avec un "+"
Cela vous semble t-il bon ? car je ne suis pas sûre de toutes mes simplifications..
- 05 Mar 2013, 21:51
- Forum: ✎✎ Lycée
- Sujet: probleme equation differentielle
- Réponses: 16
- Vues: 1249
complexe dm
Et oui 5 ans plus tard, toujours les mêmes pbs.. Bon j'ai bien vu qu'il y avait une équation du 2nd degrés: z²cos²(;))-2zsin(;))cos(;))+1=0 et donc qu'il fallait calculer delta, mais je peux pas le faire avec toutes ces inconnues..?? Comment je calcule le module et les arguments du coup ? Un petit c...
- 05 Mar 2013, 15:44
- Forum: ✎✎ Lycée
- Sujet: probleme equation differentielle
- Réponses: 16
- Vues: 1249
- 8 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
