Forum de Mathématiques: Maths-Forum

ampholyte a écrit:Je ne suis ni prof, ni un passionné de math, ni un étudiant, un simple développeur avec des connaissances de bases suffisantes pour pouvoir débloquer quelques personnes .

Oui c'est sur que moi les bases ...

Vous êtes qui en fait ? Un prof ? Un passionné de maths ? Un étudiant ?

ampholyte a écrit:Euh, pourquoi se compliquer la vie ?

Ahhh ! Merci !
:king2:

Peux-tu redonner ton problème car je ne te suis plus du tout :D D'accord, c'est encore dans mon pentagone régulier http://imageshack.us/photo/my-images/62/dscf6421w.jpg/ Je dois exprimer sin \hat{CEH} en fonction de AC/CD J'ai trouvé sin \hat{CEH} = CH/CE = [CB/2] / CE = [CD/2] / CA car le pentagon...

A une autre longueur en AC/CD

Non en fait ce sont plus des rapports ... :euh:

ampholyte a écrit:Bon alors quel est le but de l'exercice ? Pourquoi cherches-tu à faire ça ? J'ai dû mal à comprendre ce que tu cherches à faire en essayant de factoriser par AC/CD

Je voudrais exprimer une longueur en AC/CD pour pouvoir la comparer

:wrong:
Je suis désolée je ne vois pas comment mettre AC/CD en facteur ...

ampholyte a écrit:Pourquoi ne par partir comme ça

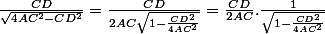
:we: Ah oui merci ! Je ne voyais pas comment sortir AC de la racine ...

Ah il faudrait que je factorise par AC ...

Je ne sait pas s'il y a des questions stupides mais je sens que j'en déterre une :help: Est t-il possible d'exprimer cette fraction : \frac{CD}{\sqrt{4AC^{2}-CD^{2}} en AC/CD ? J'ai commencé à décomposer mais je ne vois pas comment cela pourrait aider ... \frac{CD}{\sqrt{(2AC-CD)(2AC+CD&...

Je ne sais pas comment clore la discussion mais on m'a aidée, la réponse :
* D'une part ABEC losange : EC=AC
* D'autre part BCDEF pentagone régulier : CB=CD

Ainsi DF/CB = AC/CD

[FONT=Book Antiqua]Je ne sais pas comment clore la discussion mais on m'a aidée, la réponse :
* D'une part ABEC losange : EC=AC
* D'autre part BCDEF pentagone régulier : CB=CD

Ainsi DF/CB = AC/CD

[/FONT]

Coucou !
Bon, mon énigme est-elle si difficile que ça ? Pensez vous que c'est d'un niveau de première ?

Je désespère ...

Thalès lycée 1ere S (DF) // (CB) (DC) et (FB) sécantes en A http://imageshack.us/photo/my-images/62/dscf6421w.jpg/ Justifier que AD/AC = DF/CB = AC/CD Je ne vois comment prouver que AD/AC= AC/CD J'ai fait quelques recherches en décomposant AD en AC+AD mais ca ne m'avance pas : j'obtiens alors AC+CD/...

Mouais ... je ne vois toujours pas :hum:

MErci
Bon il ya des gribouillis sur la figure, et les couleurs c'est un peu ma manie ...
http://imageshack.us/photo/my-images/62/dscf6421w.jpg/

annick a écrit:Sinon, pour faire un peu d'humour à cette heure tardive, je dirai "Ah ! Je vois, on ne nous dit pas tout !!!" :ptdr:

Oui ^^ Je vais d'ailleurs aller dormir moi, je laisse décanter cette nuit en espérant y voir plus clair demain ... :dodo:

Je crois avoir trouvé mais je ne sais pas comment rédiger ... Rappel : On a les rapports égaux AC/AD = AB/AF = CB/CF soit AD/AC = AF/AB = DF/CB il faut prouver que AD/AC = AC/CD Posons AD/AC = AC/AD * (AD/AC)² De la meme manière, AC/CD = ( AC/CD ) [COLOR=DarkOrange]/ (AD/AC)²[/COLOR]