Forum de Mathématiques: Maths-Forum

Bonne année à toutes et à tous !

Salut !

Soit la bienvenue ici, j'espère que tu passeras de bon moments ici

Salut ! Selon moi ce que tu as fait me semble pas mal, mais je ne saurais pas te confirmer à 100% que c'est correct : je ne suis pas un expert en topologie hélas... Une idée qui m'a traversé l'esprit, ce serait d'essayer de montrer la contraposée. : d'après moi, si on suppose que A n'est pas dénombr...

Salut ! Énoncé tel quel, cela n'a pas de sens puisque, par définition, ce que l'on appelle le "sup" s'applique à une partie X (non vide) d'un ensemble E (partiellement ordonné), et il s'agit du plus petit des majorants de X dans E . Peut-être peux-tu nous donner un énoncé plus précis ?

Coucou,

Merci beaucoup à vous deux, ça me fait vraiment plaisir

Salut !

Soit la bienvenue sur ce forum, j'espère que tu pourras y trouver l'aide dont tu as besoin

Salut ! La somme s'effectue sur l'ensemble des couples (i,j)\in \{1,2,...,n\} tels que i\le j . Or à j fixé compris entre 1 et n , i est compris entre 1 et j donc \sum_{1\leq i \leq j \leq n } (i+j) = \sum_{j=1 }^n \bigg[ \sum_{1\le i \le j} (i+j) \bigg]= \sum_{j=1 }^n \bigg[...

Salut !

Qu'entends-tu par "résoudre cette intégrale" ?
Que signifie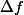 et que désigne ?
Merci d'ajouter un "contexte" à ton problème. Pour l'instant il est insolvable tel quel.

Le problème au lycée, c'est qu'on n'a pas toujours les bonnes notions pour justifier correctement les choses dans le domaine de l'analyse combinatoire. On se contente de "faire avec les mains" et on essaie de faire appel au "bon sens". A priori il faudra soit chercher sur le net,...

Salut ! En distribuant on a (x+y) (x+y)^p =x (x+y)^p+ y (x+y)^p= \underbrace{\sum_{k=0}^p \binom p k x^{k {\bf \color{red} +1}} y^{p-k}}_{=S_1} + \underbrace{ \sum_{k=0}^p \binom p k x^k y^{p-k {\bf \color{red} +1}}}}_{=S_2} Or le but va être de rassembler ces deux so...

Salut !

Que désigne l'ensemble ?
C'est quoi un endomorphisme "anti--linéaire" ?

Salut !

Je te souhaite la bienvenue sur ce forum et espère que tu pourras pleinement t'épanouir ici

L'intégrale proposée n'a aucun sens... Il n'y a pas de " dr " et d'après ce qui est écrit les variable r et \theta seraient "indépendantes", ce qui est clairement faux d'après le dessin. Par exemple, quand on prend \theta entre 0 et \pi/6 , on voit bien que r sera compris entre q...

Non, le domaine sur lequel on intègre est le disque unité auquel on enlève le disque centré en et de rayon .


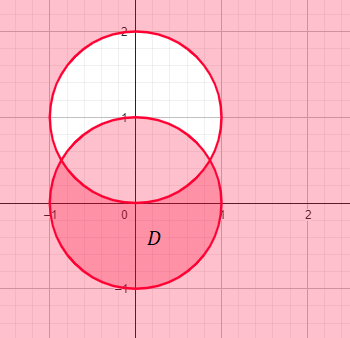
(C'est la zone la plus foncée)

Attention, le dessin est bon, mais 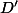n'est pas le "carré" .
Si tu pose et alors le nouveau domaine 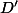sera formé de couple , pas de couples .

Salut ! Sans même se représenter le domaine d'intégration, les " x^2+y^2 " incitent fortement à utiliser un changement de variable en coordonnées polaires. En posant x:=r \cos(\theta) et y:=r \sin(\theta) , avec r\ge 0 et \theta \in [0,2\pi] , montre alors que J= \iint_{D&#...

Salut !

Il y a le polycopié du Lycée Louis-Le-Grand (lien pour le télécharger ici). Il est disponible gratuitement et est un des rare document que j'ai pu trouvé permettant de préparer de manière autodidacte l'entrée en classe prépa en seulement deux mois (pendant l'été).

Salut !

Les suites et sont définies par récurrence donc une idée serait de partir de

Salut ! Bonjour, à p donné, la somme des termes sur \lfloor\sqrt{k}\rfloor\!=\!p vaut \frac{2(-1)^p}{p} , car on somme sur un ensemble fini de cardinal (p+1)^2-1-p^2=2p . Même la série de terme général \frac{(-1)^p}{p} est une série alternée convergente, on ne peut pas conclu...

Salut !

1. On veut montrer que . Pour cela, justifie à l'aide de la réciproque du théorème de Thalès que les points , et sont alignés.
2. Montre alors en appliquant le théorème de Thalès sur deux triangles que et .