Algèbre linéaire / analyse complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par matheuxendetresse » 22 Sep 2024, 17:11
par matheuxendetresse » 22 Sep 2024, 17:11
Bonjour,
Si on veut démontrer que:
 \oplus \overline{End_{\mathbb{C}}}(C)} \cong End_{\mathbb{R}} (C))
Comment on peut décomposer un endomorphisme de
)
en endomorphismes

-linéaire et anti-

-linéaire?
-
ComeDuRondeau
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Juil 2019, 12:59
-
 par ComeDuRondeau » 22 Sep 2024, 21:20
par ComeDuRondeau » 22 Sep 2024, 21:20
Bonjour,
Avez-vous essayé de faire une analyse-synthèse ? Ce genre de raisonnement est souvent efficace pour établir des sommes directes.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 23 Sep 2024, 11:10
par capitaine nuggets » 23 Sep 2024, 11:10
Salut !
Que désigne l'ensemble

?
C'est quoi un endomorphisme "anti-

-linéaire" ?
 par matheuxendetresse » 24 Sep 2024, 13:22
par matheuxendetresse » 24 Sep 2024, 13:22
capitaine nuggets a écrit:Salut !
Que désigne l'ensemble

?
C'est quoi un endomorphisme "anti-

-linéaire" ?
Salut,
Oui,

c'est les complexes, mais c'est mal tapé, et un endomorphisme anti-

-linéaire

c'est tel que si
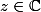
 = \overline{z} f(1))
 par matheuxendetresse » 24 Sep 2024, 13:35
par matheuxendetresse » 24 Sep 2024, 13:35
ComeDuRondeau a écrit:Bonjour,
Avez-vous essayé de faire une analyse-synthèse ? Ce genre de raisonnement est souvent efficace pour établir des sommes directes.
Oui, un peu:
J'ai écrit

où

est linéaire et

antilinéaire.
 = zh(1) +\overline{z}g(1))
Ok j'ai compris, en écrivant les images de

et de

on obtient un système simple pour trouver

et

en fonction de

Je vous remercie.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
?
-linéaire" ?