Forum de Mathématiques: Maths-Forum

globule rouge a écrit:Oui si l'on parle en degrés ! ^^ Car tu verras plus tard que car ...

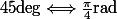
Bon ben alors oui , on parle en degrés ^^ Radian je verrai en 3ème

chan79 a écrit:au collège, on écrit par exemple cos 60°= 1/2 ou (cos 60°)²=1/4

A bon ? 60° = 1/2 ?
Savais' pas ...

globule rouge a écrit:Oui, il s'agit d'un réel quelconque !

D'accord merci bcp Une dernière petite question : Quand il faut mettre (cos(x))² , en valeur numérique , ( je prend un nombre " au pif " ) cela donnerais : (cos45)²
?? :hein2:

Elerinna a écrit:C'est tout bonnement la mesure d'un angle au centre du cercle interceptant un arc de la longueur de son rayon.

Ok , j'ai pas tout compris mais je le découvrirai bien assez tôt Merci !

Très bien :) Mais quelques petites choses sont à corriger : sin(x) ou cos(x), et non pas cos et sin tout court ! Ce sont des fonctions, qui s'appliquent donc sur des réels mais toutes seules, elles n'ont pas de sens. Aussi, on écrit cos²(x) ou (cos(x))²... Par contre, cos x² pourrait suggérer cos(x...

J'ai trouvé quelque chose : cos=AB/BC ( AB sur BC ) sin=AC/BC ( BC est l'hypothénuse ) cos B² + sin B² ( Sinus B² = cos C² ) = AB²/BC² + AC²/BC² = AB² + AC² / BC² = BC²/BC² = 1 Un nombre divisé par lui même vaudra tj 1 Ps : On peut affirmer que AC² + AB² = BC² d'ou le théorème de pythagore Estce jus...

globule rouge a écrit:tu peux nommer les côtés du triangle rectangle a, b et c et y effectuer les opérations relatives au cosinus.
Tu finiras par trouver 1, comme l'a indiqué Chan...

Je sais que je trouverais 1 , maintenant comment le prouver concrètement ? :help:

Bonjour Julie A mon avis \fra{\pi}{2}-x ne doit pas être compréhensible au collège car ils ne voient que les degrés je pense qu'il faut dessiner un triangle ABC rectangle en A et calculer (cos B)²+(cos C)² avec les rapports de longueur " Avec les rapports de longueur " ... Je sais que ça ...

Bonjour Julie A mon avis \fra{\pi}{2}-x ne doit pas être compréhensible au collège car ils ne voient que les degrés je pense qu'il faut dessiner un triangle ABC rectangle en A et calculer (cos B)²+(cos C)² avec les rapports de longueur Merci pour toutes vos expliquations ... Maintenant, je vais ess...

globule rouge a écrit:Oui, je voulais le suggérer mais j'ai complètement oublié qu'ils ne voient pas le radian au collège ^^

Le radian ? Qu'estce que c'est ?

Bonjour , C'est un dm niveau 4eme Je ne l'ai pas compris et s'il vous plaît aidez moi ! Le DM est le suivant : Avec ta calculatrice , calcule (cos30°)au carré + (cos60°)au carré ; puis (cos20°)au carré + (cos70°)au carré . Quelle conjecture peux tu faire ? Démontre que cette conjecture est vraie. Ai...