Forum de Mathématiques: Maths-Forum

Comment ça, "vérifié"?

Bonjour,

Dans le cas d'une série de fourier avec f, une fonction impaire, pourquoi avons-nous:

au lieu de ?

merci

Bonsoir ev85,

en faîte c'est le pi/2 qui me gène.
Je l'aurais eu en question dans un DS, j'aurais juste mis la première solution sans penser à la deuxième.

Bonjour,

Donc sin2 appartient à [0,1], donc pourquoi on a l'autre solution?

Bonsoir, C'est un exo de physique mais avec une question d'ordre mathématique: On a : \frac{dg}{v_{0}^2 = sin2\alpha (d, distance, g la pesanteur et v la vitesse). Pourquoi on a dans l'intervalle [0, pi/2] deux solutions et non pas une seule? \alpha = \frac{1}{2}arcsin(dg/v0^2) et \alpha =\p...

Bonjour, Je souhaite démontrer: \sum_{k=1}^n coskt = \frac{-1}{2} + \frac{sin(n+\frac{1}{2})t}{2sin(t/2)} J'y suis presque, mais je ne vois pas pourquoi je ne parviens pas à aboutir au bon résultat: \sum_{k=1}^n coskt = Re (\sum_{k=1}^n e^{ikt}) Re (\sum_{k=1}^n e^{ikt}&#...

Bonsoir,

Je cherche à factoriser dans C .

J'ai donc: X=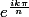 avec k = {0,...2n-1}. Peut-on avoir:

k = {-n,...,n-1} pour ensuite poser k' = -k de manière à introduire le conjugué? Est-ce juste?

Merci.

On cherche une primitive de 1/1+t² dans C. C'est dans mon cours.

Bonjour,

Quel changement de variable a-t-on effectué pour parvenir à cette égalité:



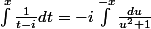
Merci.

Ok merci! :we:

Bonjour, J'essaye de m'entraîner sur les DLs et j'aimerais comprendre pourquoi on peut ici sommer deux équivalents: on a a_n = ln(1+\frac{(-1)^n}{\sqrt{n}}) - \frac{1}{2}ln(1+\frac{1}{n}) = \frac{(-1)^n}{\sqrt{n}} - \frac{1}{n} +o(\frac{1}{n}) On peut sommer d...

Ok Merci le_chat

Bonjour,

Je souhaites démontrer: .

Quelqu'un peut me donner une piste? Je suis parti de et mais ça ne me donne aucun résultat.

Si on a un x² au numérateur par exemple, on a toujours:

=

en gros, seuls a,b et c changent. Mais la décomposition reste la même?

La décomposition en éléments simples n'est pas à mon programme, alors je me suis renseigné sur Internet.
Ce que je veux dire c'est que le terme au numérateur (réel, monôme en x/x² ou polynôme) ne change rien à la décomposition?

On a toujours:

= ?

Si on avait au numérateur 2, ou x, ou x², on aurait toujours cette décomposition?

Merci.

Vous pourriez détailler svp?
Quand je veux poser b=0, je n'ai plus le b puisque j'ai du bx²

b=1/3

mais pour le x, on fait comment?

J'ai beau refaire les calculs je trouve toujours b=-1/3 et c=2/3... mais le x au numérateur me pose problème.

Ah oui j'ai fais un erreur de calcul. Pour le premier terme, j'ai au numérateur: -x +2 avec b = -1/3.

Mais alors comment dois-je procéder pour avoir l'expression désirée?