400 résultats trouvés
Revenir à la recherche avancée
Salut amis des maths ,

est un polynôme de degré
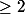
avec des coefficients rationnels.
_{n\geq 1)
est une suite de nombres rationnels telle que
=a_n)
Montrer que la suite

est périodique ... Merci de votre attention

- par MMu
- Hier, 01:01
-
- Forum: ⚔ Défis et énigmes
- Sujet: Rationnel Difficile
- Réponses: 0
- Vues: 25
Soit l’entier

.
Montrer que le polynôme

, où

, n’a pas de racine rationnelle.

- par MMu
- 08 Oct 2025, 13:09
-
- Forum: ⚔ Défis et énigmes
- Sujet: Irrationnel
- Réponses: 0
- Vues: 1204
Mea culpa (erreurs de rédaction) : manifestement il faut
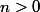
et


- par MMu
- 15 Aoû 2025, 17:05
-
- Forum: ⚔ Défis et énigmes
- Sujet: DIFFICILE
- Réponses: 4
- Vues: 1642
Soit
)
un polynôme de degré

à variable et coefficients réels, tel que
|\leq 1)
Montrer que
|\leq 2^{n-1}x ^n)

- par MMu
- 14 Aoû 2025, 01:11
-
- Forum: ⚔ Défis et énigmes
- Sujet: DIFFICILE
- Réponses: 4
- Vues: 1642
minimoy40 a écrit:Est-ce que tu as trouvé la solution au final ?
;)
À qui tu t'adresses ?

- par MMu
- 13 Avr 2025, 16:48
-
- Forum: ⚔ Défis et énigmes
- Sujet: Rationnels
- Réponses: 5
- Vues: 1470
Soit l’entier
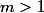
. Trouver les réels strictement positifs

tels que pour tout entier

on ait

=rationnel.

- par MMu
- 16 Mar 2025, 11:28
-
- Forum: ⚔ Défis et énigmes
- Sujet: Rationnels
- Réponses: 5
- Vues: 1470
J’avais mis
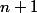
pour avoir un résultat sympa obtenu par des techniques élémentaires ...

- par MMu
- 01 Fév 2025, 11:42
-
- Forum: ⚔ Défis et énigmes
- Sujet: Calculer
- Réponses: 8
- Vues: 1190
Il est intéressant de voir que le résultat reste valable dans tout corps commutatif...

- par MMu
- 01 Fév 2025, 10:07
-
- Forum: ⚔ Défis et énigmes
- Sujet: Calculer
- Réponses: 8
- Vues: 1190
Pas de coquille. Le fait d’utiliser des techniques d'analyse (

) risque de cacher certaines choses.

- par MMu
- 01 Fév 2025, 01:01
-
- Forum: ⚔ Défis et énigmes
- Sujet: Calculer
- Réponses: 8
- Vues: 1190
Soient les entiers
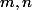
tels que

et soient

nombres complexes distincts
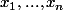
Calculer
^m}{\prod_{i\neq k}(x_k-x_i)})
.
- par MMu
- 27 Jan 2025, 11:28
-
- Forum: ⚔ Défis et énigmes
- Sujet: Calculer
- Réponses: 8
- Vues: 1190
.Soient n fonctions intégrables(Riemann) f_1,...,f_n:[0,1]\rightarrow R^+ (réels >0 ) et soient les réels positifs a_1...,a_n et les réels négatifs b_1,...,b_n . Montrer que : \int_0^1\prod_{k=1}^n{(f_k(x))^{a_kb_k}}dx\geq \prod_{k=1}^n{(\int_0^1(f_k(x))^{a_k}dx&#...
- par MMu
- 20 Déc 2024, 22:53
-
- Forum: ⚔ Défis et énigmes
- Sujet: Inégalité d’intégrales
- Réponses: 1
- Vues: 1318
Un problème que j’ai déjà posé ailleurs ... sans solution ..
Soit un entier

. On définit la suite
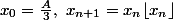
Existe-t-il toujours un

entier

(

= partie entière)

- par MMu
- 23 Sep 2024, 22:10
-
- Forum: ⚔ Défis et énigmes
- Sujet: Conjecture !?
- Réponses: 1
- Vues: 995
.Salut amis des math, voici un petit défi. Soit une suite x_0,x_1,...,x_n,... définie par la récurrence x_{n+2}=\frac{A+x_{n+1}^2}{x_n} avec A,x_0,x_1 entiers strictement positifs. Montrer que tous les termes de la suite x_n sont entiers Si et Seulement Si A+x_0^2+x_1^2 est divisible par x_0x_1 :fri...
- par MMu
- 08 Sep 2024, 22:38
-
- Forum: ⚔ Défis et énigmes
- Sujet: Suite d’entiers
- Réponses: 1
- Vues: 1044
[quote="Ben314"]Moi, ça me semble aussi O.K., mais la méthode ne marche que parce que la "barre" \alpha\!<\!1/3 . Alors que j'aurais tendance à penser que, si on part d'un irrationnel \omega (ici \sqrt{2} ) et d'un entier b\!\geqslant\!2 (ici 3), alors la suite des parties fracti...
- par MMu
- 25 Juil 2024, 20:00
-
- Forum: ⚔ Défis et énigmes
- Sujet: Suite d’entiers
- Réponses: 8
- Vues: 1372
C’est assez facilement démontrable.....

Voir un problème voisin déjà vu ici il y a quelques jours

- par MMu
- 24 Juil 2024, 01:11
-
- Forum: ⚔ Défis et énigmes
- Sujet: Suite d’entiers
- Réponses: 8
- Vues: 1372
La démarche de Ben est très différente de la mienne , et je suis très intéressé de la voir marcher. Pour l’instant je ne suis pas convaincu...

- par MMu
- 23 Juil 2024, 15:08
-
- Forum: ⚔ Défis et énigmes
- Sujet: Suite d’entiers
- Réponses: 8
- Vues: 1372
Montrer que la suite

(

entier > 0) contient une infinité de termes de la forme

(

entier > 0)

- par MMu
- 23 Juil 2024, 03:27
-
- Forum: ⚔ Défis et énigmes
- Sujet: Suite d’entiers
- Réponses: 8
- Vues: 1372









 Utilisez les sommes de Riemann
Utilisez les sommes de Riemann 
 (
(




