Forum de Mathématiques: Maths-Forum

Merci beaucoup, mais j'espère être capable de réussir cela a force d'entrainement..
Néamoins je vous remercie de votre aide pour m'aider a résoudre cet exercice, qui me montre que je dois en faire d'autres.

Bonjour, je suis toujours sur cet exercice mais je suis bloquer dans la simplification de l'équation.
Je n'arrive pas a simplifier mon pour qu'il concorde avec votre équation..

Alors j'ai fait tout ça....
0 1
-2 -1
-2-4 -3--2
-2 1-+2
01+ +2
01
est donc vraie.

Merci mais une petite question comment est apparus le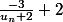
Quand a prouver que la formule soit comprise entre 0 et 1 je ne vois que la possibilité de résoudre l'inéquation..

Hé bien j'y arrive avec la formule mais après je ne vois pas comment continuer...

Avec votre formule j'y arrive mais avec la formule de départ je n'y arrive pas.

Donc, il faut démontrer que,
01
soit, 01
C'est exact?

C'est prouver que 01

C'est a dire prouver que la propriété est vrai pour k fixé dans
Et au rang k+1 c'est prouver que elle est vérifiée quelque soit k.

J'ai trouvé une méthode et tenté de l'appliquer dans ce cas présent, sur un exercice ou la suite était majorée donc sa avait l'air de concorder avec cet exercice..

Non pas du tout j'ai utilisé une méthode de résolution pour trouver ce que je venais d'écrire.

Ou sa ne donne pas quelque chose comme cela?
Fixons k, on suppose que
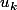est croissante donc,
Donc,
Elle est donc vérifiée au rang k+1.

Soit ?

Donc, on suppose que la proposition est vraie. Prenons k

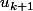
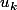
car, précédemment
C'est donc une suite croissante.

Justement la sa coince (encore plus..) car pour l'hérédité il faut formuler une hypothèse or, je n'ai pas donc, je ne vois pas trop par où chercher..

Le premier terme est 0, non?

Dans ce cas la, c'est simple car [0 ; 1]
Donc elle est automatiquement vérifié au rang 1... C'est exact?

En prenant n=0 = =
-=

Donc =

Donc,

L'initialisation consiste a prouver que est vraie.
L'hérédité consiste a démontrer la propriété au rang n+1, et la conclusion consiste à prouver que la suite est vraie au deuxième rang, donc a la confirmer.

En une étape? Je prend donc = 0,5 ?