119 résultats trouvés
Revenir à la recherche avancée
- 31 Oct 2012, 09:53
- Forum: ✎✎ Lycée
- Sujet: Fonction exponentielle
- Réponses: 4
- Vues: 386
- 30 Oct 2012, 20:01
- Forum: ✎✎ Lycée
- Sujet: Fonction exponentielle
- Réponses: 4
- Vues: 386
Fonction exponentielle
Bonjour, voilà j'ai un exercice que je dois faire mais je ne vois pas par où commencer, pouvez vous m'aidez,svp? Merci !
Voilà l'exercice:
Montrer que pour tout nombre réel x, on a:
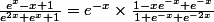
Voilà l'exercice:
Montrer que pour tout nombre réel x, on a:
- 30 Oct 2012, 19:38
- Forum: ✎✎ Lycée
- Sujet: Fonction exponentielle
- Réponses: 4
- Vues: 386
- 30 Oct 2012, 18:00
- Forum: ✎✎ Lycée
- Sujet: Dérivée d'une fonction exponentielle
- Réponses: 8
- Vues: 686
- 30 Oct 2012, 17:52
- Forum: ✎✎ Lycée
- Sujet: Dérivée d'une fonction exponentielle
- Réponses: 8
- Vues: 686
- 30 Oct 2012, 17:48
- Forum: ✎✎ Lycée
- Sujet: Dérivée d'une fonction exponentielle
- Réponses: 8
- Vues: 686
- 30 Oct 2012, 17:33
- Forum: ✎✎ Lycée
- Sujet: Dérivée d'une fonction exponentielle
- Réponses: 8
- Vues: 686
Dérivée d'une fonction exponentielle
Bonjour, je n'arrive pas à dériver la fonction, pouvez vous m'aider svp, merci!
a) (3x+7)e^-x/2
b) (x+2)e^3x
a) (3x+7)e^-x/2
b) (x+2)e^3x
- 30 Oct 2012, 17:27
- Forum: ✎✎ Lycée
- Sujet: Dérivée d'une fonction exponentielle
- Réponses: 8
- Vues: 686
- 15 Sep 2012, 23:34
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
- 15 Sep 2012, 23:10
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
Ah d'accord, j'ai compris...Merci bieber ^^
Il me reste de conclure en dressant le tableau de variation
Mais comment peut-on faire pour que l'inégalité de bernouilli est vrai?
Il me reste de conclure en dressant le tableau de variation
Mais comment peut-on faire pour que l'inégalité de bernouilli est vrai?
- 15 Sep 2012, 23:02
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
Oui, g'(x) est croissante, et même strictement croissante. Tu peux le voir en calculant g''(x) et en vérifiant que g''(x)>0. g"x)= n*(n-1)*(1+x)^n-2 = n²-n* (1+x)^n-2 c'est ça? Ah oui, et quand tu m'as dit que g'(0)=-1, dans mon énoncé c'est calculer g(0) est ce que la valeur reste la même?
- 15 Sep 2012, 22:47
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
- 15 Sep 2012, 22:37
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
Kikoo <3 Bieber a écrit:Ce que Luc veut te dire, c'est que la condition "f est définie sur R+" ne sert à rien pour déterminer les variations d'une fonction.
Comment est-ce qu'on fait alors pour étudier les variations une fois qu'on dérive la fonction?
- 15 Sep 2012, 22:23
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
- 15 Sep 2012, 22:16
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
- 15 Sep 2012, 22:15
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
- 15 Sep 2012, 22:07
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
- 15 Sep 2012, 15:24
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
- 15 Sep 2012, 15:19
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
Attention, tu n'as pas de le droit de passer de la première ligne à la deuxième. Oublie ce calcul, lis mon post précédent. Il te reste à montrer que g(\alpha_n) >0 PS : il n'y a pas de récurrence dans que ce que je t'ai dit :we: Je n'ai pas compris comment tu as fait pour montrer que g'(0)=...
- 15 Sep 2012, 14:59
- Forum: ✎✎ Lycée
- Sujet: DM sur l'inégalité de Bernouilli
- Réponses: 36
- Vues: 4509
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
