Forum de Mathématiques: Maths-Forum

Dinozzo13 a écrit:Je vois pas pourquoi !
Tu fais la somme du produits des abcisses, ordonnées et côtes :++:

Certes, mais cette somme est égale à 0.!
Juste pour montrer que les vecteurs AM et BM sont orthogonaux.

Je me perds...

AM.BM = x(x-10) + y(y-3) + z(z-4) + 29
(=) x(x-10) + y(y-3) + z(z-4) + 29 = 0

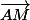
Dinozzo13 a écrit:Quelles sont les coordonnées des vecteurs et ?

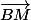
AM (x-4 ; y-1 ; z-3) et BM (x-6 ; y-2 ; z-1)

Je suis désolée, mais je ne vois pas comment avec les vecteurs ont peut déterminer une équation cartésienne de la sphère.
:/

ev85 a écrit:Que peux-tu dire du produit scalaire ?

Eh bien il est nul.

Le triangle AMB est rectangle.
Mais en quoi cela peut-il nous aider à résoudre l'exercice.?

Bonjour Nous disposons de A (4;1;3), B (6;2;1), K milieu de [AB], [AB] diamètre de la sphère ;). 1. a. Déterminer une équation cartésienne de ;). Centre. Rayon. b. Déterminer une équation cartésienne du plan tangent à A. 2. On note ;) l'ensemble des points M (x;y;z) tels que MA² + MB² = 10 a. Montre...

J'ai compris, merci beaucoup.!

Ah, et après ... < 4-3/(Un) < ...
et ... correspondent à gauche 2 (ou 2.5) à et à droite à 3.
c'est cela.?

je suppose que c'est u(n+1)=4-3/u(n) u(1)=4-3/2=2.5 on peut conjecturer que 2.5 =1 ... <1/u(n)< ... ... < 3/u(n) < ... ... < -3/u(n) < ... J'avoue que je ne vois pas là.!

Bonjour,
J'ai un problème, il faut que je démontre par récurrence que 2 ;) Un ;) 3, sachant que U0 = 2, et que Un+1 = 4-(3/n).
Il faut de plus que je conjecture le comportement de cette suite, mais comment faire.?
Merci beaucoup d'avance.

Ce n'est pas grave, merci bien quand meme.!

Je pense que tu t'es trompé pour la valeur de C.
d'après l'équation de la tangente, y=f'(a)(x-a)+f(a),
cette tangente l'est pour Cf en 0, on a y=f(0)(x-0)+f(0),
Or, f(0)=;)C et f'(0)=C,
donc y=;)Cx+C
Ainsi, C;)=(1/3) équivaut à ;)=(1/6) et C=2
non.?

Merci, mais comment exprimer f(x) en fonction de x dans ce cas.?

(1/3)x+2=0 équivaut à x=-6

En posant une équation.?

f'=C;)*e(;)x)

Donc f' = ;)*e(;)x).?

Il me faut f'(x) pour calculer C, mais comment le trouver.?