73 résultats trouvés
Revenir à la recherche avancée
Je me faisais justement la réflexion. :p C'est amusant de voir des gens parler de télépathie sur un forum de maths, lol Content d'avoir partager ce moment avec vous aussi. ;) Je continue de faire des exercices là. J'en suis aux valeurs absolues. Ca me semble simple comme principe, mais je vois pas t...
- 17 Déc 2012, 20:38
- Forum: ✎✎ Lycée
- Sujet: Calcul d'équations
- Réponses: 14
- Vues: 643
- 17 Déc 2012, 19:08
- Forum: ✎✎ Lycée
- Sujet: Calcul d'équations
- Réponses: 14
- Vues: 643
Ok merci. :lol3: Et sinon je voulais savoir, quelle est la bonne formulation ? -"l'ensemble des solutions de l'équation est..." -"la solution de l'équation est..." -"les solutions de l'équation sont..." ou bien les trois ? (pour des raisons différentes ?) Désolé de chipoter, si ça se trouve ça n'a a...
- 17 Déc 2012, 18:51
- Forum: ✎✎ Lycée
- Sujet: Calcul d'équations
- Réponses: 14
- Vues: 643
Ah oui mince, évidemment je peux pas avoir 0 au dénominateur. :marteau:
Ce serait donc plutôt S = R-{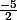 }
}
Bref dans notre cas, pour que l'équation soit nulle, il faut que x = 4.
La bonne conclusion serait donc :
L'ensemble des solutions de l'équation est S = {4}
Est-ce cela ?
Ce serait donc plutôt S = R-{
Bref dans notre cas, pour que l'équation soit nulle, il faut que x = 4.
La bonne conclusion serait donc :
L'ensemble des solutions de l'équation est S = {4}
Est-ce cela ?
- 17 Déc 2012, 18:27
- Forum: ✎✎ Lycée
- Sujet: Calcul d'équations
- Réponses: 14
- Vues: 643
Calcul d'équations
Bonjour, J'aimerais savoir ce que je suis censé faire sur cette équation : \frac{x-4}{2x+5}=0 On sait qu'un produit de facteurs est nul si et seulement si un de ses facteurs est nul. Mais là j'ai un doute car il ne s'agit pas d'un produit mais d'une fraction. Aurais-je ceci : x-4=0 et 2x+5=0 soit : ...
- 17 Déc 2012, 17:44
- Forum: ✎✎ Lycée
- Sujet: Calcul d'équations
- Réponses: 14
- Vues: 643
- 08 Déc 2010, 10:39
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
- 07 Déc 2010, 20:45
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
@Nightmare : oui oui on est d'accord ! :lol3:
@Sylviel : N'est-ce pas plutôt a et b les réels et i le nombre imaginaire ?
@Sylviel : N'est-ce pas plutôt a et b les réels et i le nombre imaginaire ?
- 07 Déc 2010, 20:28
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
Je vais peut-être dire un truc un peu faux, mais dans l'esprit, avoir : 4x + 5 c'est un peu comme avoir 4x \times 1 + 5 \times 1 Et on peut voir que les chiffres 1 sont imaginaires. C'est un peu ça les nombres complexes, non ? C'est comme lorsqu'on a : 4x-1 = 0 En fait, on a les nombres "imagin...
- 07 Déc 2010, 20:10
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
@Sylviel : Effectivement, l'intuition est ce qui est certainement le plus utile, même en maths. Mais voilà, ça ne fait pas tout !De plus, d'une classe à une autre, d'une génération à une autre, on a des programmes un peu différents, ou du moins établis différemment. Du coup, on demande parfois des ...
- 07 Déc 2010, 19:09
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
Whoa ! Je vois qu'il y a eu pleins d'interventions. Alors, je vais tenter de répondre un peu à chacune : @Doraki : Si tu as bien lu mes posts, tu verras que je pose et repose des tas de questions pour bien comprendre toutes les notions du monde merveilleux des complexes ! :zen: Et surtout, ce mystér...
- 07 Déc 2010, 17:25
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
On peux représenter les complexes comme les points du plan, et non plus seulement d'une droite (les réels). Et multiplier par i devient alors une rotation de pi/2. Du coup i²= 1*i*i. Donc tu prends le point 1 (c'est à dire de coordonées (0,1)) et tu lui fais faire deux rotations successives de pi/2...
- 07 Déc 2010, 08:35
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
Merci pour toutes vos explications sur les complexes !
Depuis quelques jours que je poste sur ce forum, ça m'aide bien.
Vos réponses sont constructives et comprendre les choses fait
que j'aime de plus en plus les mathématiques ! :zen:
Depuis quelques jours que je poste sur ce forum, ça m'aide bien.
Vos réponses sont constructives et comprendre les choses fait
que j'aime de plus en plus les mathématiques ! :zen:
- 06 Déc 2010, 18:19
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
Eh bah voilà, là c'est logique ! C'est explicable ! donc je réponds :
j'obtiens le point de coordonnées (0;-1). Par rotation, je suis tombé sur l'ordonnée -1
J'ai bon ?
j'obtiens le point de coordonnées (0;-1). Par rotation, je suis tombé sur l'ordonnée -1
J'ai bon ?
- 06 Déc 2010, 18:11
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
la différence, c'est que 4 ça existe déjà, et que c'est définit comme étant positif. Oui, c'est vrai, le carré d'un nombre réel est positif. Maintenant, est-ce incohérent de parler d'un nombre i tel que i² = -1 ? La réponse est non, à partir du moment où l'on décide que i n'est pas un nombre réel. ...
- 06 Déc 2010, 17:50
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
l'ensemble C des nombres complexe se construit, mais c'est encore beaucoup plus dur à démontrer son existence ainsi que ce qu'il contient... Ca, ça m'intrigue. Je suis en terminale ! ^^ Et je fais de grandes révisions là, parce que je suis pas trop au point. J'aimerais avoir une bonne note au bac !...
- 06 Déc 2010, 17:44
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
Oui, je comprends, en règle générale d'ailleurs, on a inventé les mathématiques, mdr. Mais on ne peut pas non plus inventer n'importe quoi. Moi aussi, je pourrais dire : Tiens à partir d'aujourd'hui, 4 sera un négatif. Mais on aurait un peu de mal à comprendre pourquoi, si un jour j'ai x = 4 - 2 Est...
- 06 Déc 2010, 17:28
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
Bon, je dirais que pour le raisonnement, je comprends, mais je n'ai pas encore tout compris d'un point de vue théorique : 1. Pourquoi i^2 = -1 (en fait, pourquoi un nombre négatif, vu que i est un carré ?) 2. Mis à part pour nous faire apprendre le cours, à quoi ça sert les complexes dans la vie ? P...
- 06 Déc 2010, 17:16
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
Donc en fait, dans R (ensemble des réels), 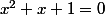 n'a pas de solutions (car discriminant négatif)
n'a pas de solutions (car discriminant négatif)
Et, dans C (ensemble des complexes),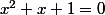 peut être résolu.
peut être résolu.
Avoir cette équation :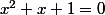 c'est donc comme avoir cette équation :
c'est donc comme avoir cette équation : 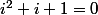 ?
?
Et, dans C (ensemble des complexes),
Avoir cette équation :
- 06 Déc 2010, 17:04
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
Génial ! Qui mieux que le fondateur de la notation des complexes peut répondre à mes questions ! :we: Bon, alors oui je me doute que c'est un truc à apprendre par coeur. Mais je me demande toujours pourquoi ? Après tout, un carré n'est-il pas toujours positif ? Si oui, alors comment i^2 peut être ég...
- 06 Déc 2010, 16:47
- Forum: ✎✎ Lycée
- Sujet: Complexes : i² = -1 (pourquoi ?)
- Réponses: 47
- Vues: 8576
- 73 résultats trouvés - Page 1 sur 4 • 1, 2, 3, 4
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
