15 résultats trouvés
Revenir à la recherche avancée
.
...........
- 03 Juin 2008, 14:52
- Forum: ⚖ Place de marché
- Sujet: .
- Réponses: 1
- Vues: 875
- 07 Mar 2008, 20:26
- Forum: ✯✎ Supérieur
- Sujet: Somme d'une série
- Réponses: 2
- Vues: 623
Somme d'une série
Bonjour tout le monde..
Voila cet exercice m'enerve car je sens qu'il est tres simple....
Calculer3^{n}}}) .
.
Ya t-il quelqu'un qui pourrait me debloquer....
Voila cet exercice m'enerve car je sens qu'il est tres simple....
Calculer
Ya t-il quelqu'un qui pourrait me debloquer....
- 07 Mar 2008, 19:58
- Forum: ✯✎ Supérieur
- Sujet: Somme d'une série
- Réponses: 2
- Vues: 623
f étant définie sur [0;1], je ne vois pas comment tu as pu utiliser les "parties parires" et "parties impaires" :++: Exact... J'ai une solution, mais elle est loin d'être immédiate. Et moi aussi, je m'attendais à plus simple... Je suis donc pas le seul à avoir ete surpris par la...
- 26 Déc 2007, 12:32
- Forum: ✯✎ Supérieur
- Sujet: integrale
- Réponses: 3
- Vues: 436
integrale
Soit f ({C}^{0}([0,1],\mathbb{R}) Montrer que \int_{-1/2}^{3/2}{f(3x^2-2x^3)dx} =2 \int_{0}^{1}{f(3x^2-2x^3)dx} . Je le poste ici pour voir votre soluce, j'ai trouvé quelquechose en decomposant f en somme de fonction paire et impaire, j'ai essayé des changements de variab...
- 25 Déc 2007, 15:41
- Forum: ✯✎ Supérieur
- Sujet: integrale
- Réponses: 3
- Vues: 436
Merci pour la reponse...
Justement cette remarque permet de traiter la premiere question mais pour la seconde question je ne vois pas comment utiliser cette remarque...
(Ou alors quelquchose m'echappe completement...)
Justement cette remarque permet de traiter la premiere question mais pour la seconde question je ne vois pas comment utiliser cette remarque...
(Ou alors quelquchose m'echappe completement...)
- 12 Déc 2007, 16:22
- Forum: ✯✎ Supérieur
- Sujet: integrabilité
- Réponses: 3
- Vues: 723
integrabilité
Bonjour ...j' essaie de faire un sujets d'oral de l'X ...il est posé en deux questions.. Soit f \mathcal{C}^{0}(\mathbb{R},\mathbb{R}) integrable. On pose pour x \neq 0 g(x)=f(x-\frac{1}{x}) . 1-Montrer que g est intégrable sur \mathbb{R} privé de 0. 2-Montrer que \int_{-\inf...
- 12 Déc 2007, 15:57
- Forum: ✯✎ Supérieur
- Sujet: integrabilité
- Réponses: 3
- Vues: 723
Densité
Bonjour les matheux...
Je bute sur une question d'un probleme (qui ne depend d'aucune autre question...):
Montrer que l'ensemble des points à coordonnées rationnelles est dense dans le cercle unité.
J'avoue que cela ne me parait pas naturel mais bon....
Pouvez vous m'aider......
Je bute sur une question d'un probleme (qui ne depend d'aucune autre question...):
Montrer que l'ensemble des points à coordonnées rationnelles est dense dans le cercle unité.
J'avoue que cela ne me parait pas naturel mais bon....
Pouvez vous m'aider......
- 07 Aoû 2007, 20:41
- Forum: ✯✎ Supérieur
- Sujet: Densité
- Réponses: 5
- Vues: 712
.
..........
- 18 Avr 2007, 15:45
- Forum: ⚖ Place de marché
- Sujet: .
- Réponses: 0
- Vues: 864
Je ne pense pas que c'est ce qu'elle attend, en fait on peut resoudre ce probleme sans une ligne de calcul mais avec un dessin .A,B et C sont les trois hauteur d'un triangle d'orthocentre D. Je te laisse finir...(pense aussi aux arguments qui doivent valoir pi/2...)
- 01 Oct 2006, 15:19
- Forum: ✯✎ Supérieur
- Sujet: Hauteurs d'un triangle sont concourantes, Complexes
- Réponses: 3
- Vues: 1021
Tu peux demontrer ce resultat par l'absurde. En effet ta remaque est judicieuse... Supposons que A=y+z et B=\sum\limits_{k=0}^{p-1}{-z}^{p-1-k}y^k ne soient pas preiers entre eux alors ils ont un diviseur premier que l'on va appeler D. Avec ta remarque on a A*B=y^{p}+z^{p}=(-x)^{p} on en ded...
- 25 Aoû 2006, 22:45
- Forum: ✯✎ Supérieur
- Sujet: Sophie Germain
- Réponses: 5
- Vues: 1123
Euh...la vraie formule que gauss a trouvé a l'age de 5 ans provient de cette remarque: 2(1+2+3+...+n)=1+2+...+n+1+2+...+n=(1+2+3+...+n)+(n+n-1+n-2+...1)=(1+n)+(2+n-1)+.....+(n+1) . Puisqu'il y a n termes entre parenthéses on en deduis le resutat.... En...
- 20 Aoû 2006, 21:38
- Forum: ✯✎ Supérieur
- Sujet: Formule du petit Gauss
- Réponses: 18
- Vues: 3182
Tout nombre est congru a la somme de ses chiffres modulo 9, il suffit juste de tester tous les cas et on a 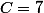 .....
.....
- 19 Aoû 2006, 15:15
- Forum: ⚜ Salon Mathématique
- Sujet: exo d'arithmetique
- Réponses: 9
- Vues: 2679
je penses que tu voulais dire a<b<c
Ouais c'est ca..j'avais oublié.
Sinon j'avais fait le même raisonnement que aviateurpilot en prenant l'ensemble
- 18 Aoû 2006, 15:09
- Forum: ⚔ Défis et énigmes
- Sujet: Exo sympa
- Réponses: 9
- Vues: 1214
Exo sympa
Soit  une bijection de
une bijection de  dans
dans  .
.
Prouver que l'on peut trouver trois entiers et
et  verifiant:
verifiant:
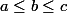 et
et  + f(c)= 2 f(b))
Prouver que l'on peut trouver trois entiers
- 17 Aoû 2006, 20:58
- Forum: ⚔ Défis et énigmes
- Sujet: Exo sympa
- Réponses: 9
- Vues: 1214
- 15 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
