Forum de Mathématiques: Maths-Forum

Car est un chiffre donc .

Si toutes tes variables sont des chiffres (i.e. des entiers de 0 à 9) alors

Salut,
Sans connaitre quoi que ce soit concernant la variable a (et, dans une moindre mesure, les autres) on ne peut pas dire grand chose : essaye avec a=150,23 ou bien -a=-0.012 voire a=-3,14159 . .

J'ai la flemme de faire le calcul, mais c'est les mêmes que ceux du paradoxe des anniversaires : d'un coté, si tu regarde uniquement deux tirage, la proba; qu'ils soient les mêmes est extrêmement faible,, mais d'un autre coté, si tu as par exemple 1 000 tirages, alors il y a 500 000 façon de les gro...

Salut, Vu la modélisation mathématique actuelle de ce qu'est "le hasard" (modélisation qui a fait largement ces preuves dans tout les domaines où elle a été utilisée), le fait qu'une certaine combinaison soit, ou ne soit pas, déjà sortie n'a absolument aucune influence concernant le fait q...

Salut,
Du fait que on a et donc

Salut. C'est uniquement un problème de définition (donc sans grand intérêt) : la tendance majoritaire à l'heure actuelle est plutôt de considérer que la terme "anneau" désigne un anneau unitaire (et d'utiliser le terme de "pseudo anneau" dans le cas non unitaire). Par contre, je ...

En fait, c'est assez immédiat : vu les n oscillations entre -1 et 1 que fait T_n sur l'intervalle |-1,1] , tout polynôme P tel que P\big([-1,1]\big)\!\subset\![-1,1] est tel que l'équation P(x)\!=\!T_n(x) admet au moins n racines (comptées avec ordre de multiplicité) sur |-1,...

Salut, J'ai l'impression que le "plus grand" polynôme de degré n vérifiant l'hypothèse est le n -ième polynôme de Tchebychev T_n : si P\!\in\!{\mathbb R}_n[X] est tel que \forall x\!\in\![-1,1],\ P(x)\!\in\![-1,1] alors \forall x\!\geqslant\!1,\ P(x)\!\leqslant\!T_n(x&#...

Ma langue à fourchée : ce que je voulais écrire n'est pas "deux cotés adjacents du carré et le centre" mais "deux sommets adjacents et le centre" où le "centre" désigne (entre autre) le point d'intersection des diagonales du carré et l’hypoténuse désigne le coté opposé ...

Salut, Le triangle formé de deux cotés adjacents du carré et de son centre est isocèle rectangle avec deux angles de \alpha/2 et une hypoténuse de a . En utilisant la relation duale de la formule des cosinus on en déduit que 0=\cos(\pi/2)=-\cos^2(\alpha/2)+\sin^2(\alpha/2)\co...

Salut, Lorsque x tend vers +\infty , f_n(x) est équivalent à \dfrac{1}{2^n}x (preuve par récurrence) donc f_n(x)\!-\!\sqrt{x} tend vers +\infty et cela prouve que la suite (f_n)_{n\geqslant 0} ne converge uniformément vers x\to\sqrt{x} sur aucun intervalle [M,+\infty[ .

Salut,
Soit j'ai pas bien compris les règles, soit 'est assez simple : le premier joueur commence par jouer pile au centre du disque puis, systématiquement, il joue à l'endroit diamétralement opposé à celui où vient de jouer son adversaire. Sa victoire est assurée.

Salut,
Par définition, un espace compact est séparé (dans la définition francophone) . . .

Salut, Si on prend par exemple p=4 (non premier) et k=2, (qui divise p) alors k divise {p\choose k}\!=\!6 . Donc il n'y a pas de contradiction à ton hypothèse. Il y a éventuellement plus simple, mais on peut commencer par montrer que, pour tout nombre premier p, la valuation p-adique de {n\choose k}...

Salut,
Lorsque tu dérive la fonction par rapport à , je ne comprend pas d'où provient ton .

Salut,
Pour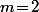 je pense avoir la preuve que la seule solution est , et je conjecturerais bien qu'il en va de même dans le cas général. Sauf que ma preuve ne me semble pas facilement généralisable à tout .

Salut, J'ai pas regardé le reste, mais si ta preuve est basé sur ça : En posant z=g(x) . . . on obtient g(f(z))=z, càd gof=I . alors c'est incomplet vu que tu ne prouve l'égalité g(f(z))=z que pour certains réels z et pas pour tous. Il faudrait avoir la surjectivité de la fonction g pour que ce soit...

Salut, Pour le (c) (par exemple), ton ensemble, c'est l'ensemble des "trucs" qui peuvent s'écrire sous la forme 1/k avec k dans N*, c'est à dire 1, 1/2, 1/3, 1/4, . . . Et très clairement, à part 1, ces "trucs ne sont pas des entiers, mais des rationnels. Et il est tout aussi claireme...

Salut, Autre exemple : An = l'ensemble des entiers naturels multiple de n. On peut aussi noter que si non seulement les intersections finies sont non vides, mais qu'on sait aussi qu'une (au moins) de ces intersection finie est de cardinal fini alors l'intersection globale est non vide. Donc les cont...