Forum de Mathématiques: Maths-Forum

Heuuuu.... je suis pas sur de bien comprendre la question.... Pour faire l'exo, j'utilise la formule que... je t'ai donné dans le post ci dessus. Si tu me demande quelle formule j'utilise pour démontrer la formule sus-nommée, ben... je suis un peu dans la m... vu que cette formule pour la démontrer...

Salut, Si \ \varphi(t)=f(u(t),v(t))\ alors \ \varphi'(t)=u'(t)\frac{\partial f}{\partial x}(u(t),v(t))+v'(t)\frac{\partial f}{\partial y}(u(t),v(t))\ A utiliser deux fois pour conclur...

Bonjour,

Pourriez-vous svp me mettre sur la voie quant à la réponse à cette question :

Soit f une application différentiable de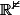 dans

Calculer la dérivée de la fonction : t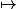 f(t, f(t,t))

Merci

Merci beaucoup radoude.

Peux tu me dire si j'ai bien rédigé stp ?

Merci de m'aider svp

Bonjour, lol désolé je me suis trompé dénoncé, cetait celui dun autre exo. Voici le bon : On sait par expérience qu'une opération chirurgicale a 90% de chances de réussir. cette opération est réalisée dans une clinique 400 fois chaque année. Soit N le nombre de réussites dans une année. 1. Quelle es...

bonjour, Voici l'énnoncé du pb : 100 chasseurs tirent indépendamment sur un même cerf. Chaque chasseur a une chance sur 10 d'atteindre sa cible. 1. Donner la loi N du nombre de balles reçues par le cerf 2. Par quelle loi peut on l'approximer ? 3. En déduire à l'aide des tables une valeur approchée d...

Il y a 2 valeurs possibles dans cet exercice, or ma calculatrice (texas collège : la seule autorisée au DAEU B) ne m'en donnera qu'une, que me conseilles-tu ?

Bonsoir,

N'y connaissant rien en trigo pour le moment, pourriez vous m'aider à résoudre cette equation svp ? Ou du moins me mettre sur la voie ?



Merci

annick a écrit:Bonsoir,
le vecteur directeur de ta droite a pour coordonnées (-b;a)
On remarque que ça marche, il est bien perpendiculaire au vecteur normal(a;b)

En effet -ab + ab = 0.

Merci annick :++:

Bonjour,

Est il possible de trouver le vercteur directeur d'une droite d'équation :
ax + by + c = 0

Je sais que le vecteur normal a pour coordonnées (a, b), mais qu'en est-il du vecteur directeur ?

Merci

je dérive x^(1/2) mais pas avec la définition x^n => nx^(n-1), avec celle-ci :
x^(1/2) => 1/(2.x^(1/2))

Il me semble que n doit faire partie des entier naturel positifs (ensemble N), Donc je pense que vous faites erreur. Il me semble qu'il faut appliquer la propriété du produit de 2 fonctions dérivables (u.v)' = u'v + uv', soit : f(x) = x.x^(1/2) donne f'(x)= 1 * x^(1/2) + x/(2.3^(1/2)) Mais maintenan...

Oui il y a une identité remarquable